Lesson 10: Changing Scales in Scale Drawings

Let’s explore different scale drawings of the same actual thing.

10.1: Appropriate Measurements

  1. If a student uses a ruler like this to measure the length of their foot, which choices would be appropriate measurements? Select all that apply. Be prepared to explain your reasoning.
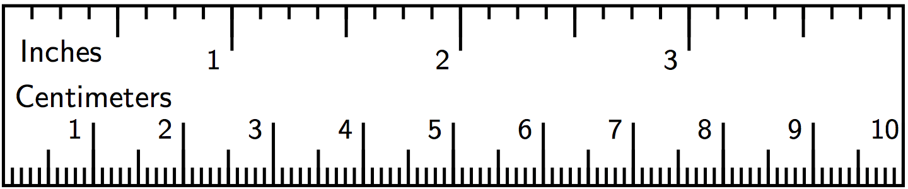
    The ruler measures inches and centimeters. The inches are broken into eighths and the centimeters are broken into tenths.

    1. $9\frac14$ inches

    2. $9\frac{5}{64}$ inches

    3. 23.47659 centimeters

    4. 23.5 centimeters

    5. 23.48 centimeters

  2. Here is a scale drawing of an average seventh-grade student's foot next to a scale drawing of a foot belonging to the person with the largest feet in the world. Estimate the length of the larger foot.

10.2: Same Plot, Different Drawings

Here is a map showing a plot of land in the shape of a right triangle.

A map that shows a plot of land indicated by a right triangle. Logan Square Map Copyright Owner: American Fact Finder License: Public Domain Via: American Fact Finder
  1. Your teacher will assign you a scale to use. On centimeter graph paper, make a scale drawing of the plot of land. Make sure to write your scale on your drawing.
  2. What is the area of the triangle you drew? Explain or show your reasoning.
  3. How many square meters are represented by 1 square centimeter in your drawing?
  4. After everyone in your group is finished, order the scale drawings from largest to smallest. What do you notice about the scales when your drawings are placed in this order?

10.3: A New Drawing of the Playground

Here is a scale drawing of a playground. 

The scale is 1 centimeter to 30 meters.

  1. Make another scale drawing of the same playground at a scale of 1 centimeter to 20 meters.
  2. How do the two scale drawings compare?

Summary

Sometimes we have a scale drawing of something, and we want to create another scale drawing of it that uses a different scale. We can use the original scale drawing to find the size of the actual object. Then we can use the size of the actual object to figure out the size of our new scale drawing.

For example, here is a scale drawing of a park where the scale is 1 cm to 90 m.

The rectangle is 10 cm by 4 cm, so the actual dimensions of the park are 900 m by 360 m, because $10 \boldcdot 90 = 900$ and $4 \boldcdot 90 = 360$.

Suppose we want to make another scale drawing of the park where the scale is 1 cm to 30 meters. This new scale drawing should be 30 cm by 12 cm, because $900 \div 30 = 30$ and $360 \div 30 = 12$.

Another way to find this answer is to think about how the two different scales are related to each other. In the first scale drawing, 1 cm represented 90 m. In the new drawing, we would need 3 cm to represent 90 m. That means each length in the new scale drawing should be 3 times as long as it was in the original drawing. The new scale drawing should be 30 cm by 12 cm, because $3 \boldcdot 10 = 30$ and $3 \boldcdot 4 = 12$.

Since the length and width are 3 times as long, the area of the new scale drawing will be 9 times as large as the area of the original scale drawing, because $3^2=9$.

Practice Problems ▶