Let’s read stories from the graphs of proportional relationships.
Here is a graph that represents a proportional relationship.
Tyler was at the amusement park. He walked at a steady pace from the ticket booth to the bumper cars.
| row 1 | time (seconds) |
distance (meters) |
|---|---|---|
| row 2 | 0 | 0 |
| row 3 | 20 | 25 |
| row 4 | 30 | 37.5 |
| row 5 | 40 | 50 |
| row 6 | 1 |
If Tyler wanted to get to the bumper cars in half the time, how would the graph representing his walk change? How would the table change? What about the constant of proportionality?
4 seagulls ate 10 pounds of garbage. Assume this information describes a proportional relationship.
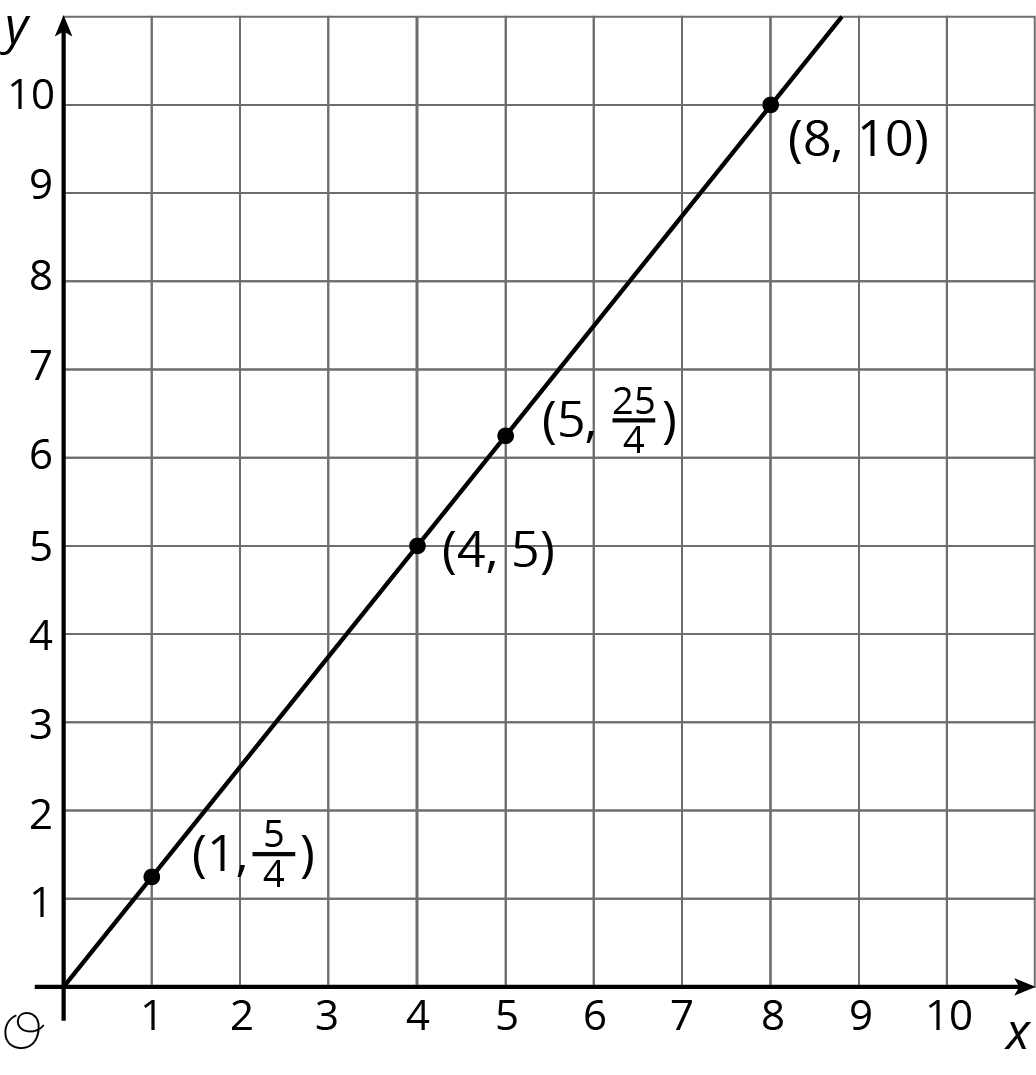
For the relationship represented in this table, $y$ is proportional to $x$. We can see in the table that $\frac54$ is the constant of proportionality because it’s the $y$ value when $x$ is 1.
The equation $y = \frac54 x$ also represents this relationship.
| $x$ | $y$ | |
|---|---|---|
| row 1 | 4 | 5 |
| row 2 | 5 | $\frac{25}{4}$ |
| row 3 | 8 | 10 |
| row 4 | 1 | $\frac{5}{4}$ |
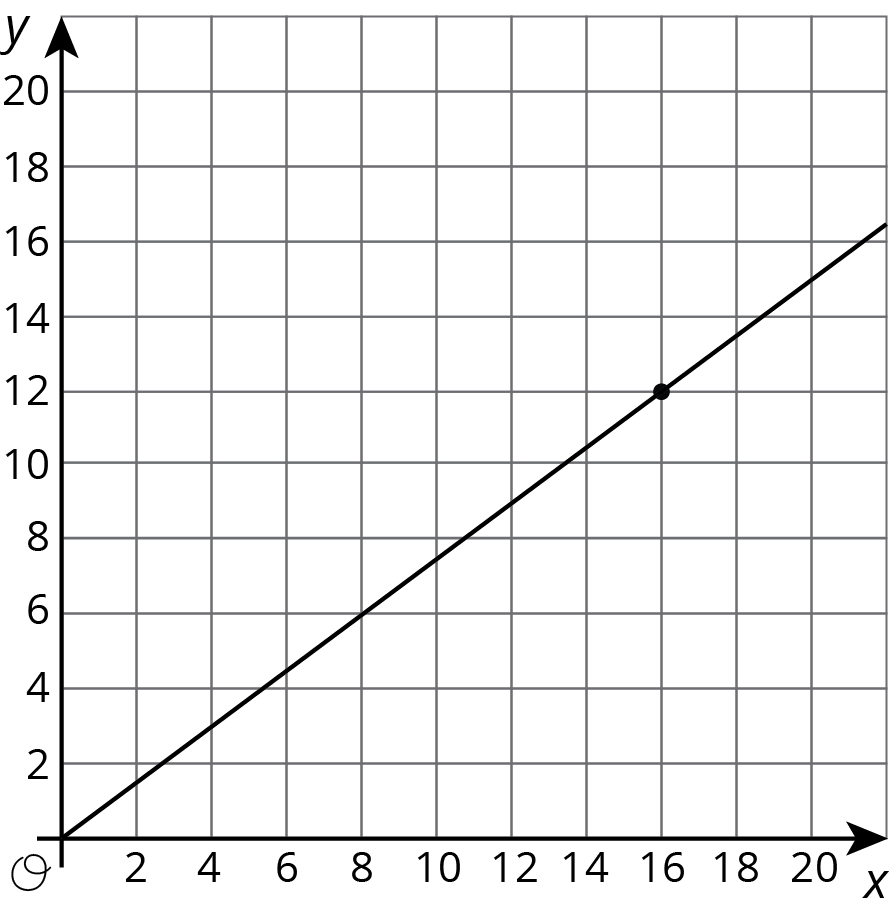
Here is the graph of this relationship.
If $y$ represents the distance in feet that a snail crawls in $x$ minutes, then the point $(4, 5)$ tells us that the snail can crawl 5 feet in 4 minutes.
If $y$ represents the cups of yogurt and $x$ represents the teaspoons of cinnamon in a recipe for fruit dip, then the point $(4, 5)$ tells us that you can mix 4 teaspoons of cinnamon with 5 cups of yogurt to make this fruit dip.
We can find the constant of proportionality by looking at the graph, because $\frac54$ is the $y$-coordinate of the point on the graph where the $x$-coordinate is 1. This could mean the snail is traveling $\frac54$ feet per minute or that the recipe calls for $1\frac14$ cups of yogurt for every teaspoon of cinnamon.
In general, when $y$ is proportional to $x$, the corresponding constant of proportionality is the $y$-value when $x=1$.
