Lesson 8: Reasoning about Solving Equations (Part 2)

Let’s use hangers to understand two different ways of solving equations with parentheses.

8.1: Equivalent to $2(x+3)$

Select all the expressions equivalent to $2(x+3)$.

  1. $2 \boldcdot (x+3) $
  2. $(x + 3)2 $
  3. $2 \boldcdot x + 2 \boldcdot 3$ 
  4. $2 \boldcdot x + 3 $
  5. $(2 \boldcdot x) + 3$ 
  6. $(2 + x)3$

8.2: Either Or

  1. Explain why either of these equations could represent this hanger:

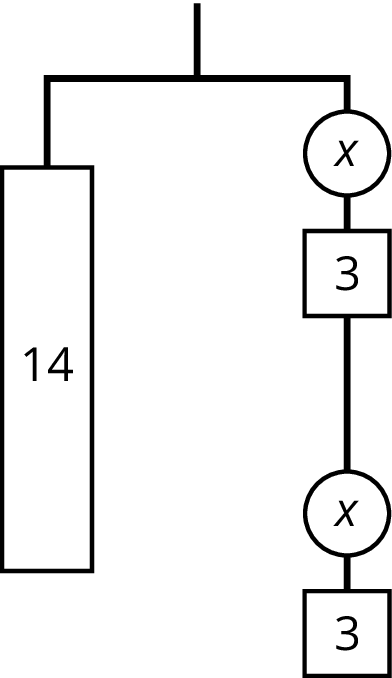
    $14=2(x+3)$ or $14=2x+6$

  2. Find the weight of one circle. Be prepared to explain your reasoning.

8.3: Use Hangers to Understand Equation Solving, Again

Here are some balanced hangers. Each piece is labeled with its weight.

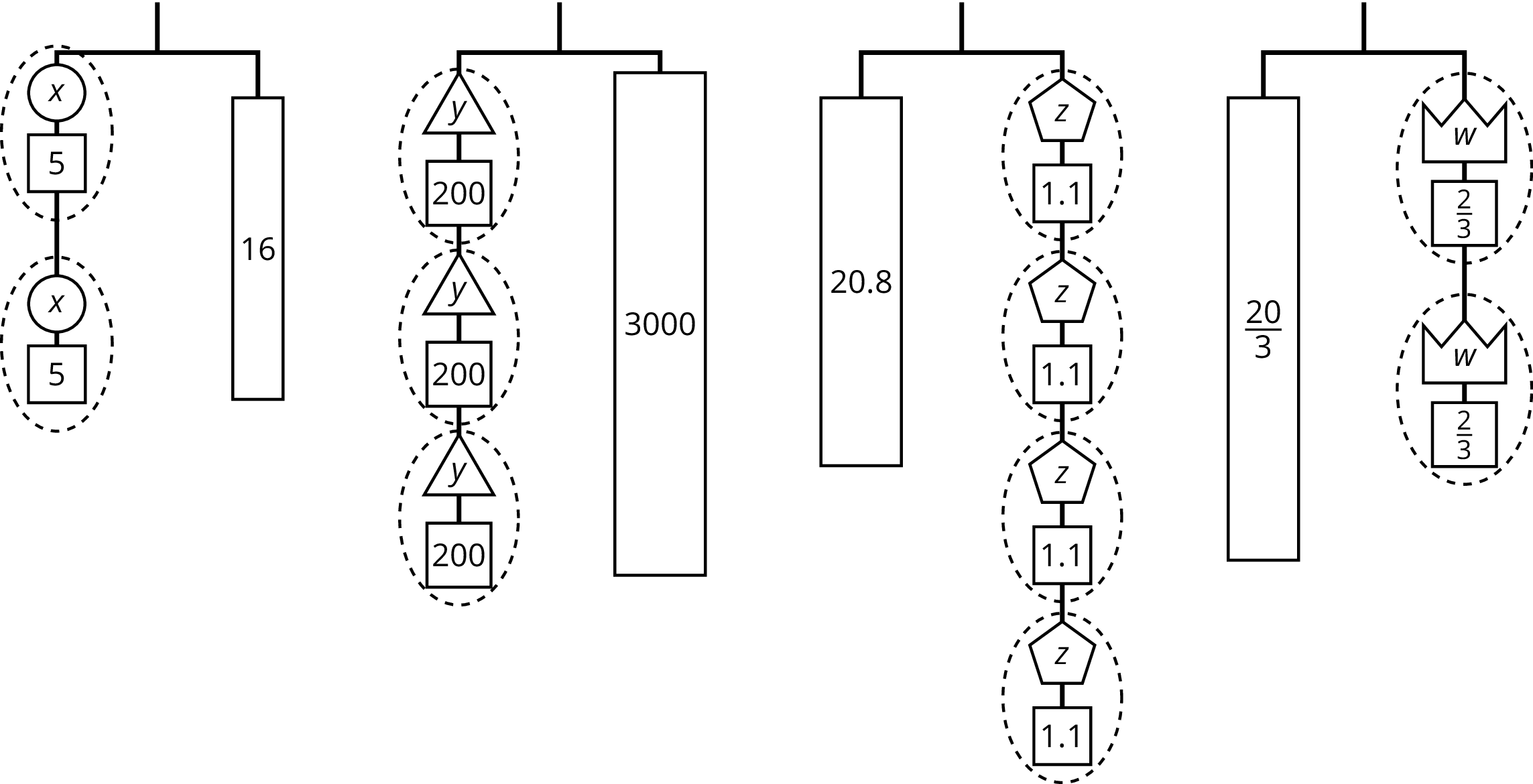
For each diagram:

  1. Assign one of these equations to each hanger: 

    $2(x+5)=16$

    $3(y+200)=3\!,000$

    $20.8=4(z+1.1)$

    $\frac{20}{3}=2\left(w+\frac23\right)$

     

  2. Explain how to figure out the weight of a piece labeled with a letter by reasoning about the diagram.
  3. Explain how to figure out the weight of a piece labeled with a letter by reasoning about the equation.

Summary

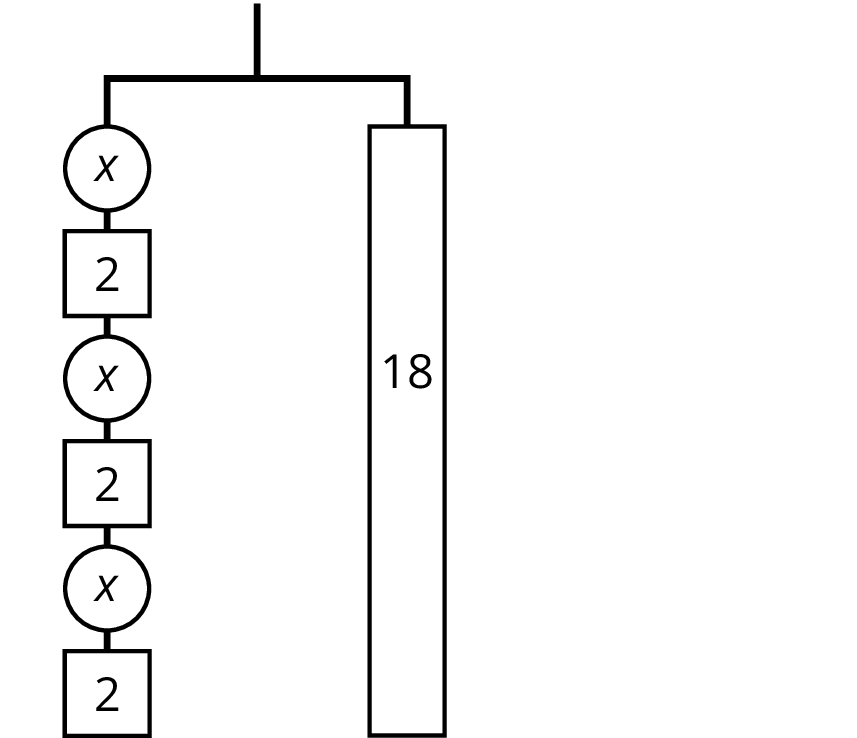
The balanced hanger shows 3 equal, unknown weights and 3 2-unit weights on the left and an 18-unit weight on the right.

There are 3 unknown weights plus 6 units of weight on the left. We could represent this balanced hanger with an equation and solve the equation the same way we did before.

\(\begin {align} 3x+6&=18 \\ 3x&=12 \\ x&=4 \\ \end{align}\)

Since there are 3 groups of $x+2$ on the left, we could represent this hanger with a different equation: $3(x+2)=18$.

The two sides of the hanger balance with these weights: 3 groups of $x+2$ on one side, and 18, or 3 groups of 6, on the other side.

 

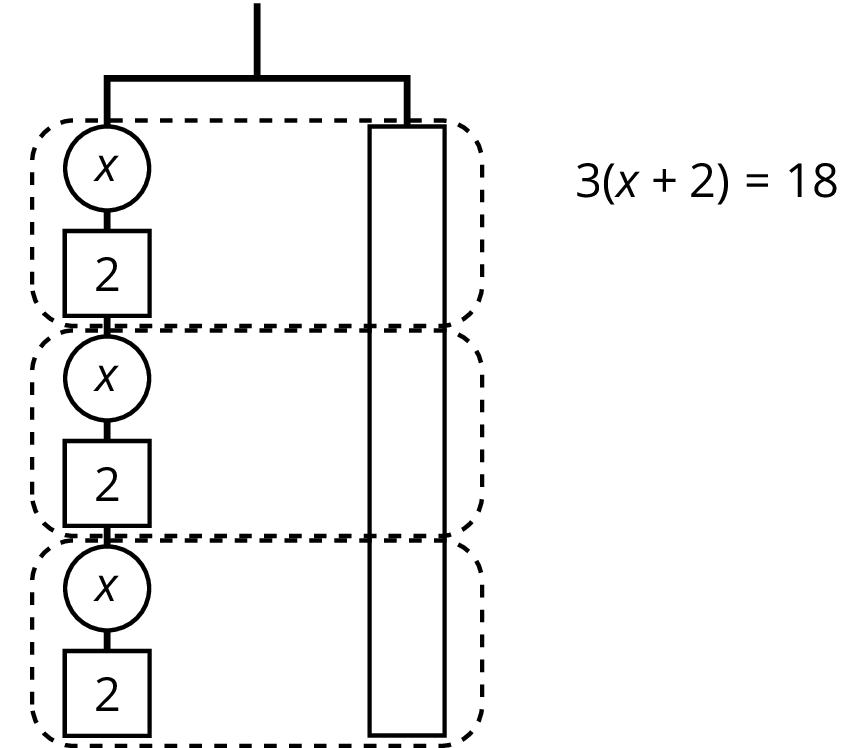
The two sides of the hanger will balance with $\frac13$ of the weight on each side: $\frac13 \boldcdot 3(x+2) = \frac13 \boldcdot 18$.

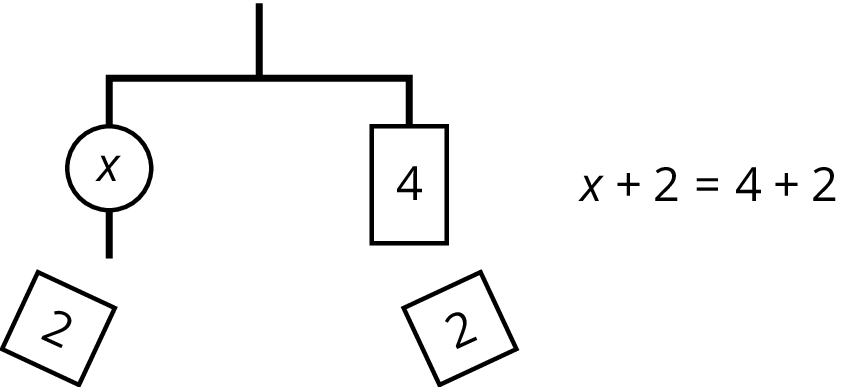
We can remove 2 units of weight from each side, and the hanger will stay balanced. This is the same as subtracting 2 from each side of the equation.

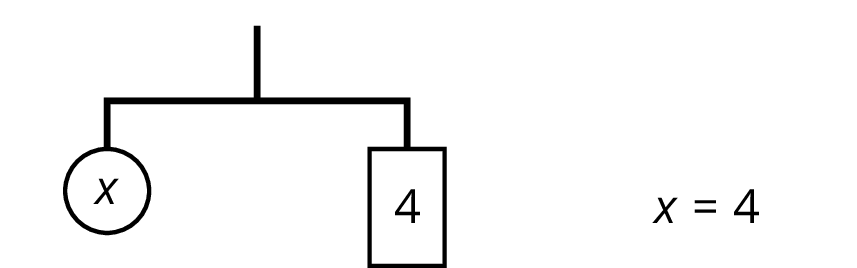
An equation for the new balanced hanger is $x=4$. This gives the solution to the original equation.

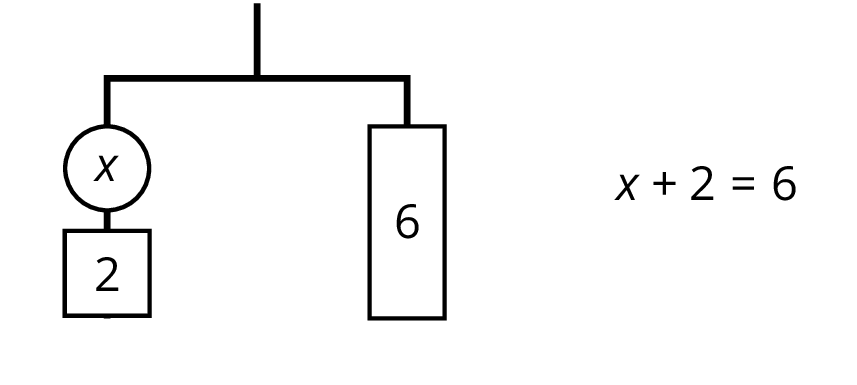
Here is a concise way to write the steps above:

\(\begin{align} 3(x+2) &= 18 \\ x + 2 &= 6 & \text{after multiplying each side by } \tfrac13 \\ x &= 4 & \text{after subtracting 2 from each side} \\ \end{align} \)

Practice Problems ▶