9.1: Number Talk: Which is Greater?
Without calculating, decide which quotient is larger.
$11 \div 23$ or $7 \div 13$
$0.63 \div 2$ or $0.55 \div 3$
$15 \div \frac{1}{3}$ or $15 \div \frac{1}{4}$
Let’s create our own scale drawings.
Without calculating, decide which quotient is larger.
$11 \div 23$ or $7 \div 13$
$0.63 \div 2$ or $0.55 \div 3$
$15 \div \frac{1}{3}$ or $15 \div \frac{1}{4}$
Noah made a rough sketch of the layout of his room (not a scale drawing).
 and the Segment tool
and the Segment tool  to draw the walls of Noah's scale floor plan in the applet.
to draw the walls of Noah's scale floor plan in the applet.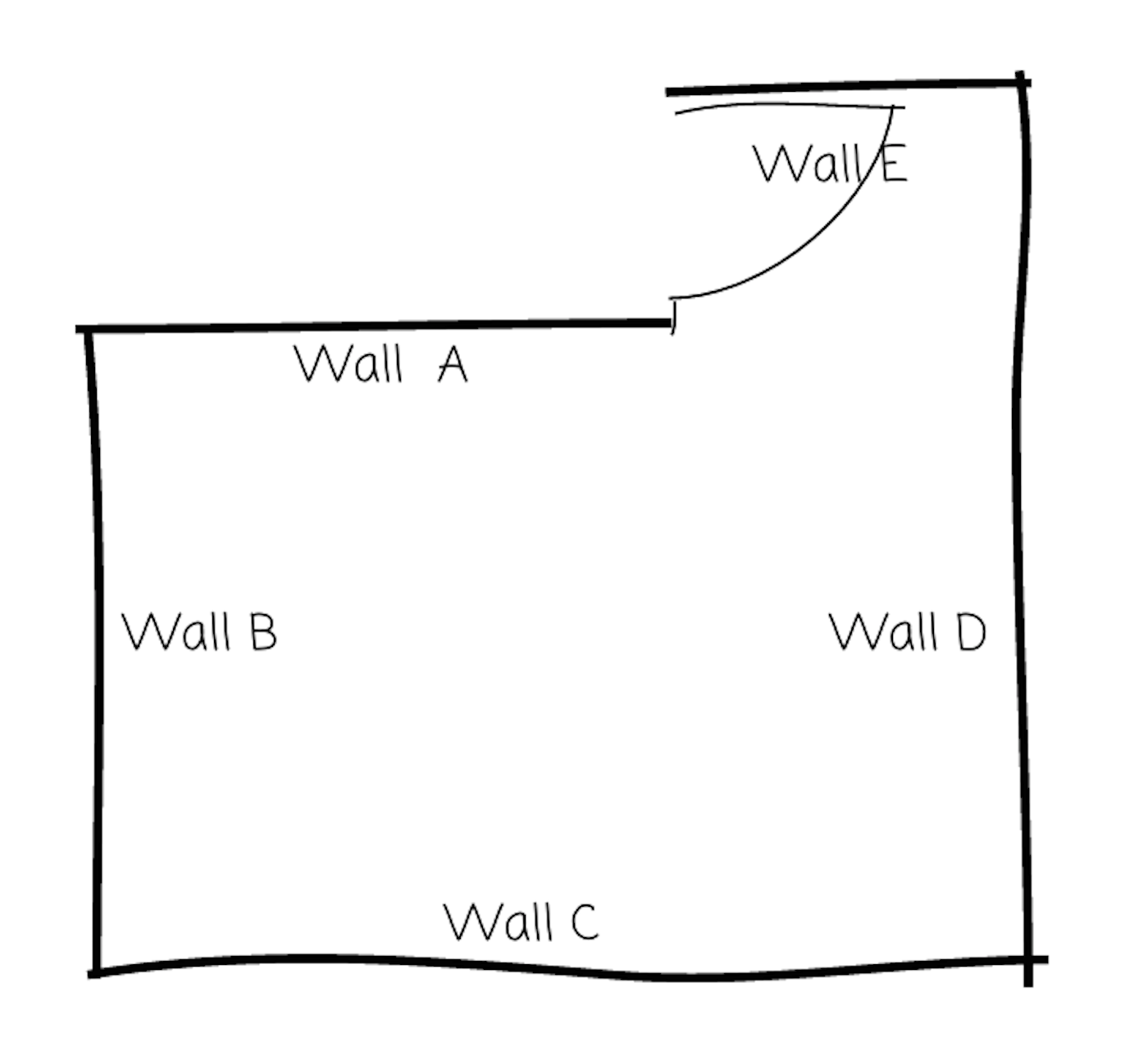
If Noah wanted to draw another floor plan on which Wall C was 20 cm, would 1 cm to 5 m be the right scale to use? Explain your reasoning.
A rectangle around Utah is about 270 miles wide and about 350 miles tall. The upper right corner that is missing is about 110 miles wide and about 70 miles tall.
Make a scale drawing of Utah where 1 centimeter represents 50 miles.
Make a scale drawing of Utah where 1 centimeter represents 75 miles.
If we want to create a scale drawing of a room's floor plan that has the scale “1 inch to 4 feet,” we can divide the actual lengths in the room (in feet) by 4 to find the corresponding lengths (in inches) for our drawing.
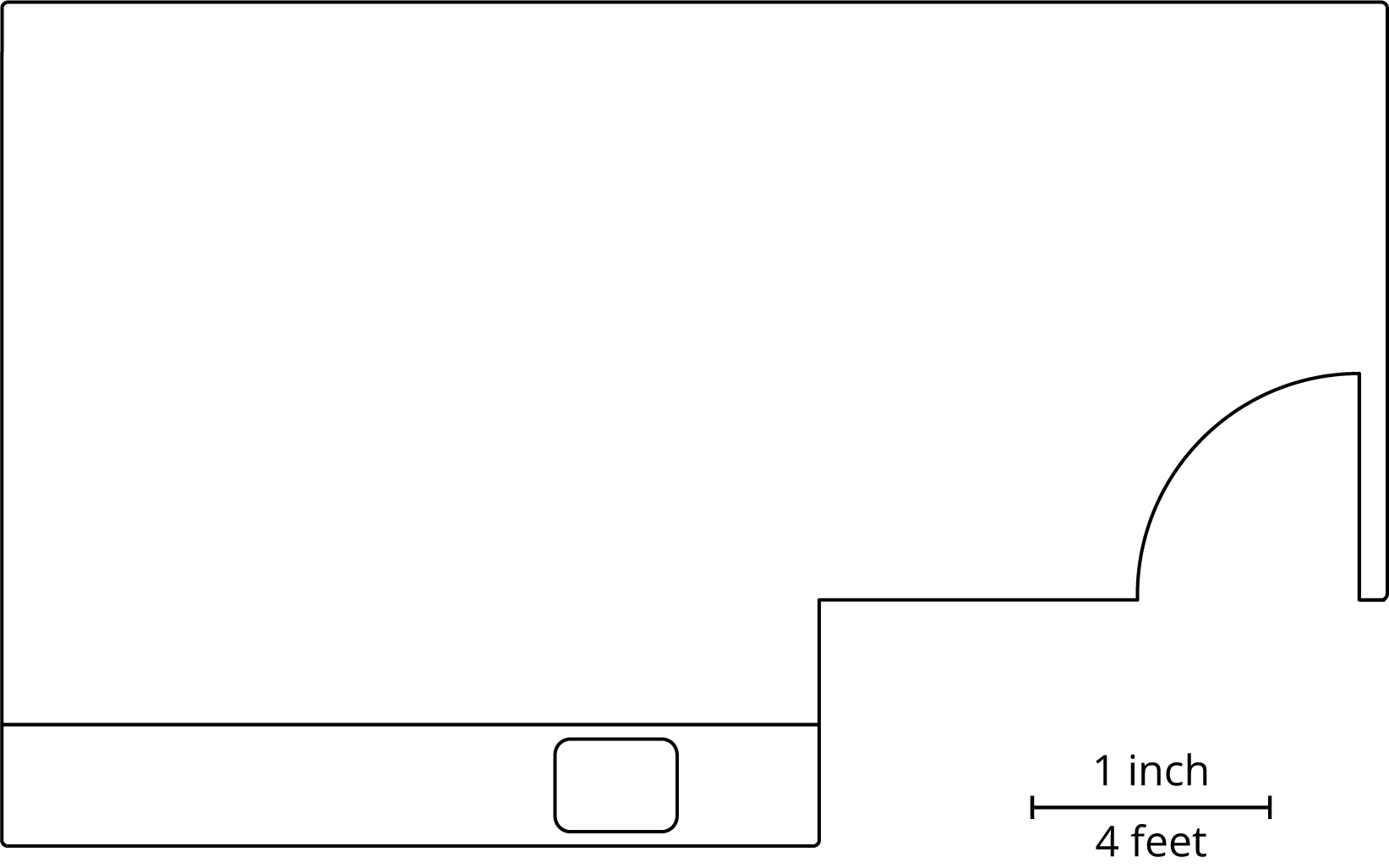
Suppose the longest wall is 15 feet long. We should draw a line 3.75 inches long to represent this wall, because $15 \div 4 = 3.75$.
There is more than one way to express this scale.
These three scales are all equivalent, since they represent the same relationship between lengths on a drawing and actual lengths:
Any of these scales can be used to find actual lengths and scaled lengths (lengths on a drawing). For instance, we can tell that, at this scale, an 8-foot long wall should be 2 inches long on the drawing because $\frac14 \boldcdot 8 = 2$.
The size of a scale drawing is influenced by the choice of scale. For example, here is another scale drawing of the same room using the scale 1 inch to 8 feet.

Notice this drawing is smaller than the previous one. Since one inch on this drawing represents twice as much actual distance, each side length only needs to be half as long as it was in the first scale drawing.