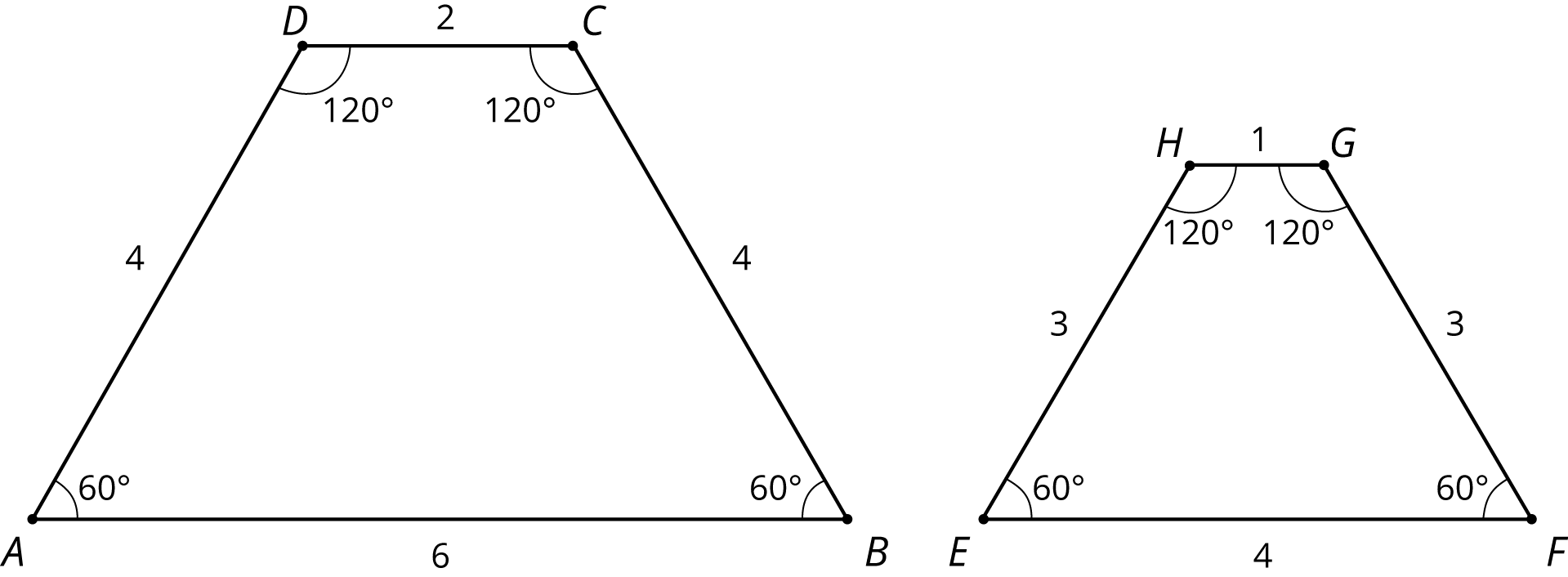
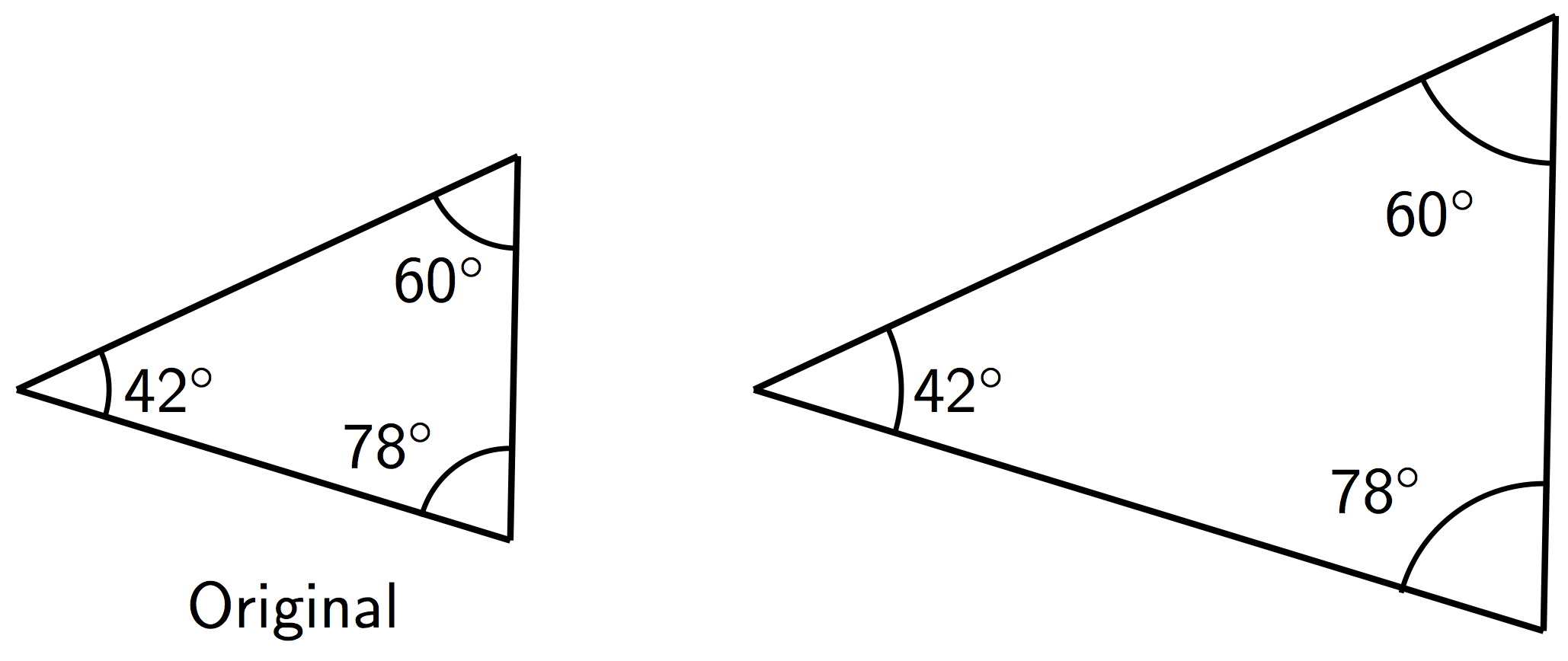
4.1: Three Quadrilaterals (Part 1)
Each of these polygons is a scaled copy of the others.

- Name two pairs of corresponding angles. What can you say about the sizes of these angles?
- Check your prediction by measuring at least one pair of corresponding angles using a protractor. Record your measurements to the nearest 5^\circ.