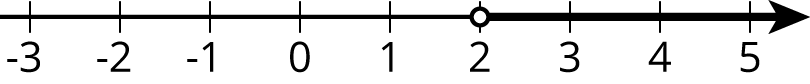Here is an inequality: $3(10-2x) < 18$. The solution to this inequality is all the values you could use in place of $x$ to make the inequality true.
In order to solve this, we can first solve the related equation $3(10-2x) = 18$ to get the solution $x = 2$. That means 2 is the boundary between values of $x$ that make the inequality true and values that make the inequality false.
To solve the inequality, we can check numbers greater than 2 and less than 2 and see which ones make the inequality true.
Let’s check a number that is greater than 2: $x= 5$. Replacing $x$ with 5 in the inequality, we get $3(10-2 \boldcdot 5) < 18$ or just $0 < 18$. This is true, so $x=5$ is a solution. This means that all values greater than 2 make the inequality true. We can write the solutions as $x > 2$ and also represent the solutions on a number line:
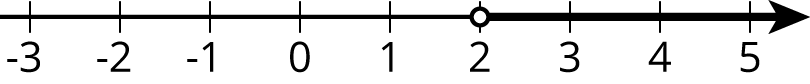
Notice that 2 itself is not a solution because it's the value of $x$ that makes $3(10-2x)$ equal to 18, and so it does not make $3(10-2x) < 18$ true.
For confirmation that we found the correct solution, we can also test a value that is less than 2. If we test $x=0$, we get $3(10-2 \boldcdot 0) < 18$ or just $30 < 18$. This is false, so $x = 0$ and all values of $x$ that are less than 2 are not solutions.