Imagine that a faucet is leaking at a constant rate and that every 2 minutes, 10 milliliters of water leaks from the faucet. There is a proportional relationship between the volume of water and elapsed time.
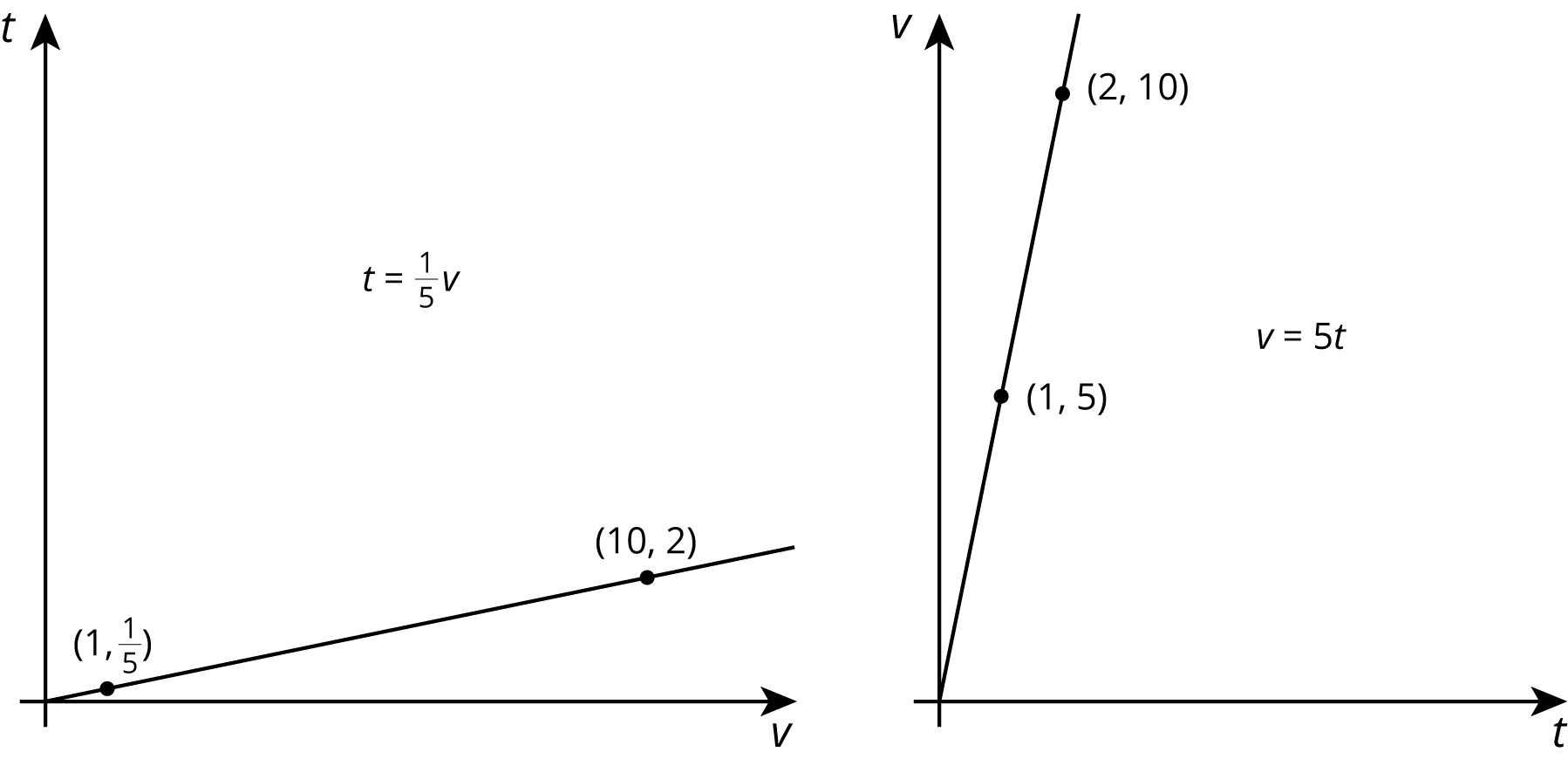
- We could say that the elapsed time is proportional to the volume of water. The corresponding constant of proportionality tells us that the faucet is leaking at a rate of $\frac15$ of a minute per milliliter.
- We could say that the volume of water is proportional to the elapsed time. The corresponding constant of proportionality tells us that the faucet is leaking at a rate of 5 milliliters per minute.
Let’s use $v$ to represent volume in milliliters and $t$ to represent time in minutes. Here are graphs and equations that represent both ways of thinking about this relationship:
Even though the relationship between time and volume is the same, we are making a different choice in each case about which variable to view as the independent variable. The graph on the left has $v$ as the independent variable, and the graph on the right has $t$ as the independent variable.