Lesson 8: Keeping Track of All Possible Outcomes

Let’s explore sample spaces for experiments with multiple parts.

8.1: How Many Different Meals?

How many different meals are possible if each meal includes one main course, one side dish, and one drink?

  main courses side dishes drinks
row 1 grilled chicken salad milk
row 2 turkey sandwich applesauce juice
row 3 pasta salad — water

8.2: Lists, Tables, and Trees

Consider the experiment: Flip a coin, and then roll a number cube.

Elena, Kiran, and Priya each use a different method for finding the sample space of this experiment.

  • Elena carefully writes a list of all the options: Heads 1, Heads 2, Heads 3, Heads 4, Heads 5, Heads 6, Tails 1, Tails 2, Tails 3, Tails 4, Tails 5, Tails 6.

  • Kiran makes a table:
  1 2 3 4 5 6
H H1 H2 H3 H4 H5 H6
T T1 T2 T3 T4 T5 T6

  • Priya draws a tree with branches in which each pathway represents a different outcome:

    A tree diagram for flipping a coin and rolling a number cube. On the first level of the tree, the two branches are “H” for heads and “T” for tails for a total of two branches. On the second level of the tree, there are 6 branches from “H” and 6 branches from “T” where each branch is labeled with a different number from 1 through 6.
  1. Compare the three methods. What is the same about each method? What is different? Be prepared to explain why each method produces all the different outcomes without repeating any.

  2. Which method do you prefer for this situation?

    Pause here so your teacher can review your work.

  3. Find the sample space for each of these experiments using any method. Make sure you list every possible outcome without repeating any.

    1. Flip a dime, then flip a nickel, and then flip a penny. Record whether each lands heads or tails up.
    2. Han’s closet has: a blue shirt, a gray shirt, a white shirt, blue pants, khaki pants, and black pants. He must select one shirt and one pair of pants to wear for the day.
    3. Spin a color, and then spin a number.

       

      Two different circular spinners. The spinner on the left is divided into four equal parts. The first part is red and labeled “R,” the second part is blue and labeled “B,” the third part is green and labeled “G,” and the fourth part is white and labeled “W.” The pointer is in the part labeled “W.” The spinner on the right is divided into five equal parts. Starting from the top right, and moving clockwise, the first part is labeled 1, the second, 2, the third, 3, the fourth, 4, and the fifth, 5. The pointer is in the part labeled “5.”

    4. Spin the hour hand on an analog clock, and then choose a.m. or p.m.

8.3: How Many Sandwiches?

  1. A submarine sandwich shop makes sandwiches with one kind of bread, one protein, one choice of cheese, and two vegetables. How many different sandwiches are possible? Explain your reasoning. You do not need to write out the sample space.

    • Breads: Italian, white, wheat
    • Proteins: Tuna, ham, turkey, beans
    • Cheese: Provolone, Swiss, American, none
    • Vegetables: Lettuce, tomatoes, peppers, onions, pickles

    Submarine sandwich and chips Copyright Owner: jeffreyw License: CC BY 2.0 Via: Wikimedia Commons

  2. Andre knows he wants a sandwich that has ham, lettuce, and tomatoes on it. He doesn’t care about the type of bread or cheese. How many of the different sandwiches would make Andre happy?

  3. If a sandwich is made by randomly choosing each of the options, what is the probability it will be a sandwich that Andre would be happy with?

Summary

Sometimes we need a systematic way to count the number of outcomes that are possible in a given situation. For example, suppose there are 3 people (A, B, and C) who want to run for the president of a club and 4 different people (1, 2, 3, and 4) who want to run for vice president of the club. We can use a tree, a table, or an ordered list to count how many different combinations are possible for a president to be paired with a vice president.

With a tree, we can start with a branch for each of the people who want to be president. Then for each possible president, we add a branch for each possible vice president, for a total of $3\boldcdot 4 = 12$ possible pairs. We can also start by counting vice presidents first and then adding a branch for each possible president, for a total of $3 \boldcdot 4 = 12$ possible pairs.

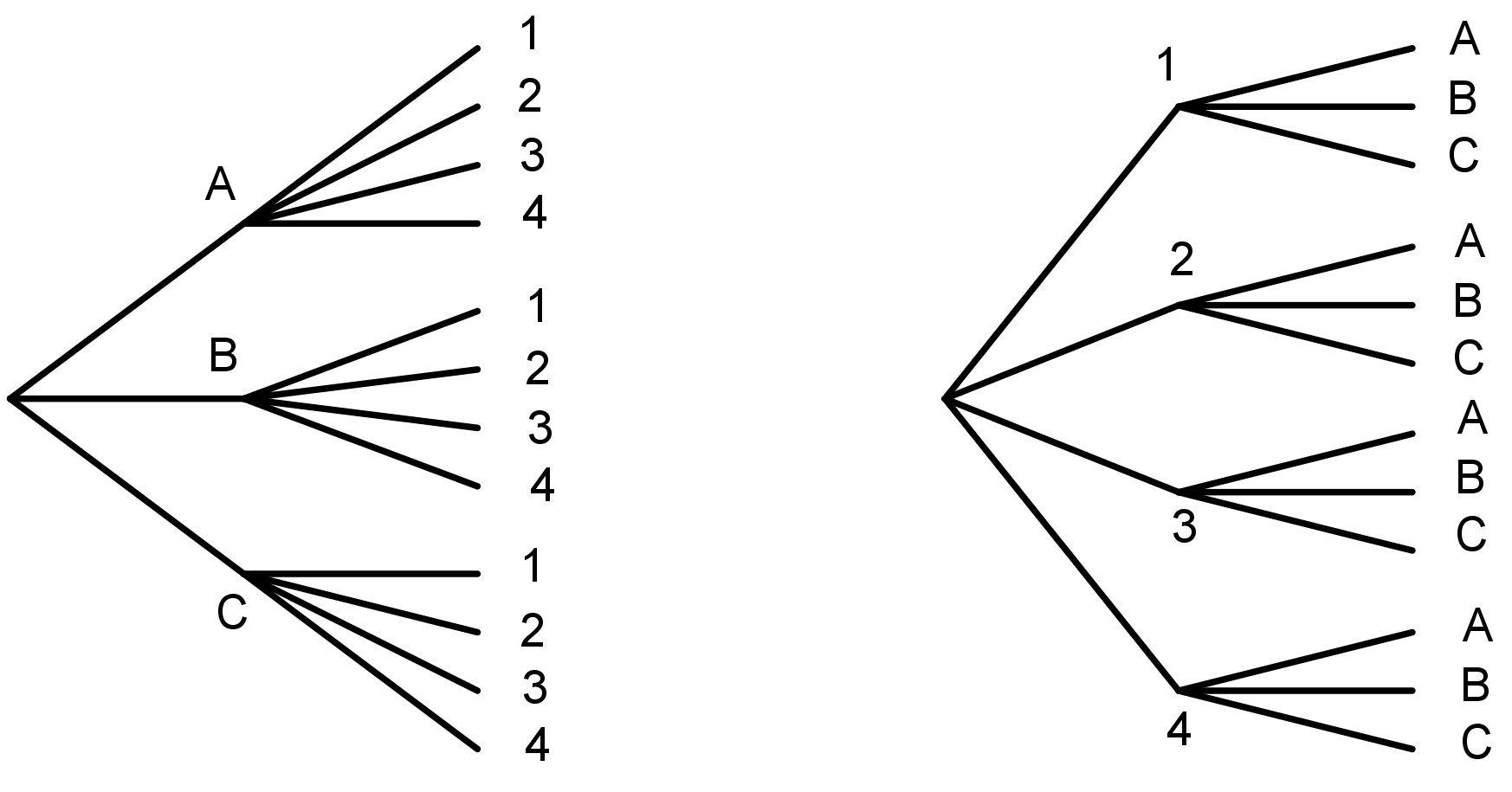
Two tree diagrams. The leftmost tree diagram has three branches for the first choice, labeled “A,” “B”, and “C.” Choices “A”, “B”, and “C” each have four branches labeled with a different number from 1 through 4. The rightmost tree diagram has four branches for the first choice, labeled 1, 2, 3, and 4. Choices 1, 2, 3, and 4 each have three branches, labeled with a different letter “A,” “B,” or “C.”

A table can show the same result:

  1 2 3 4
A A, 1 A, 2 A, 3 A, 4
B B, 1 B, 2 B, 3 B, 4
C C, 1 C, 2 C, 3 C, 4

So does this ordered list:

A1, A2, A3, A4, B1, B2, B3, B4, C1, C2, C3, C4

Practice Problems ▶