Lesson 7: Exploring the Area of a Circle
Let’s investigate the areas of circles.
7.2: Estimating Areas of Circles
Your teacher will assign your group two circles of different sizes.
- Set the diameter of your assigned circle and use the applet to help estimate the area of the circle.
Note: to create a polygon, select the Polygon tool, and click on each vertex. End by clicking the first vertex again. For example, to draw triangle $ABC$, click on $A$-$B$-$C$-$A$.
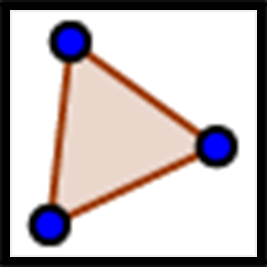
- Record the diameter in column $D$ and the corresponding area in column $A$ for your circles and others from your classmates.
-
In a previous lesson, you graphed the relationship between the diameter and circumference of a circle. How is this graph the same? How is it different?
- How many circles of radius 1 unit can you fit inside a circle of radius 2 units so that they do not overlap?
- How many circles of radius 1 unit can you fit inside a circle of radius 3 units so that they do not overlap?
- How many circles of radius 1 unit can you fit inside a circle of radius 4 units so that they do not overlap?
If you get stuck, consider using coins or other circular objects.
7.3: Covering a Circle
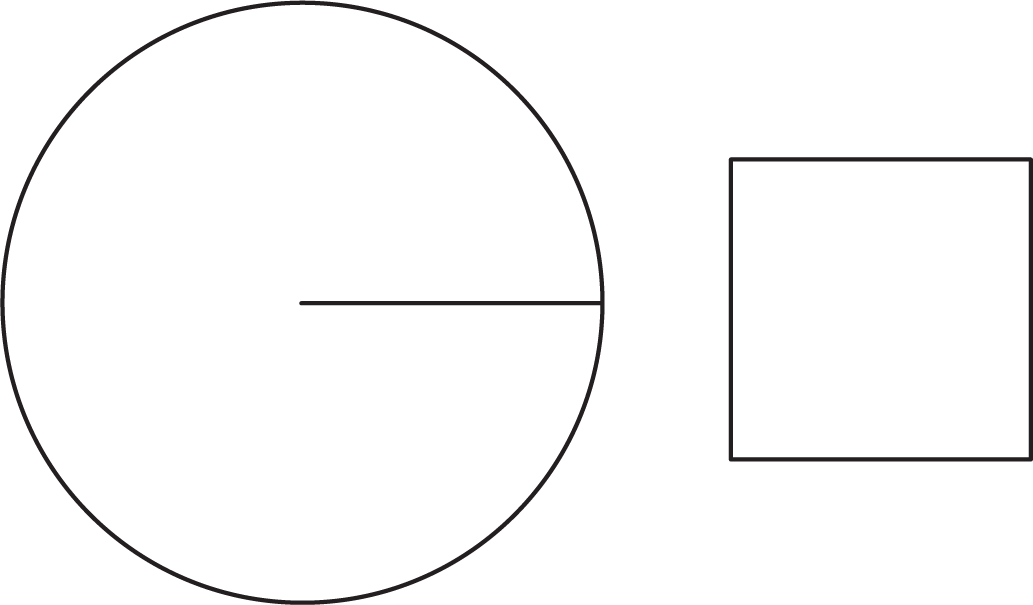
Here is a square whose side length is the same as the radius of the circle.
Summary
The circumference $C$ of a circle is proportional to the diameter $d$, and we can write this relationship as $C = \pi d$. The circumference is also proportional to the radius of the circle, and the constant of proportionality is $2 \boldcdot \pi$ because the diameter is twice as long as the radius. However, the area of a circle is not proportional to the diameter (or the radius).
The area of a circle with radius $r$ is a little more than 3 times the area of a square with side $r$ so the area of a circle of radius $r$ is approximately $3r^2$. We saw earlier that the circumference of a circle of radius $r$ is $2\pi r$. If we write $C$ for the circumference of a circle, this proportional relationship can be written $C = 2\pi r$.
The area $A$ of a circle with radius $r$ is approximately $3r^2$. Unlike the circumference, the area is not proportional to the radius because $3r^2$ cannot be written in the form $kr$ for a number $k$. We will investigate and refine the relationship between the area and the radius of a circle in future lessons.
Practice Problems ▶
Glossary
-
area of a circle
area of a circle
The area of a circle whose radius is $r$ units is $\pi r^2$ square units.