Lesson 9: Applying Area of Circles

Let’s find the areas of shapes made up of circles.

9.1: Still Irrigating the Field

The area of this field is about 500,000 m2. What is the field’s area to the nearest square meter? Assume that the side lengths of the square are exactly 800 m.

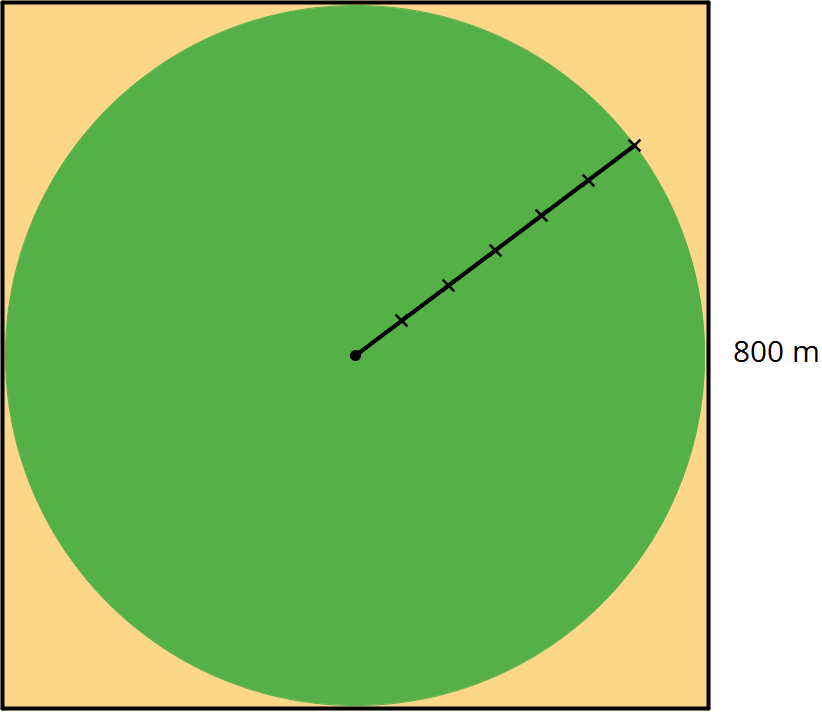
A square where the vertical distance is labeled 800 meters. The largest possible circle is drawn inside the square with a line segment is that begins from the center of the circle to a point on the edge of the circle.
  1. 502,400 m2
  2. 502,640 m2
  3. 502,655 m2
  4. 502,656 m2
  5. 502,857 m2

9.2: Comparing Areas Made of Circles

  1. Each square has a side length of 12 units. Compare the areas of the shaded regions in the 3 figures. Which figure has the largest shaded region? Explain or show your reasoning.
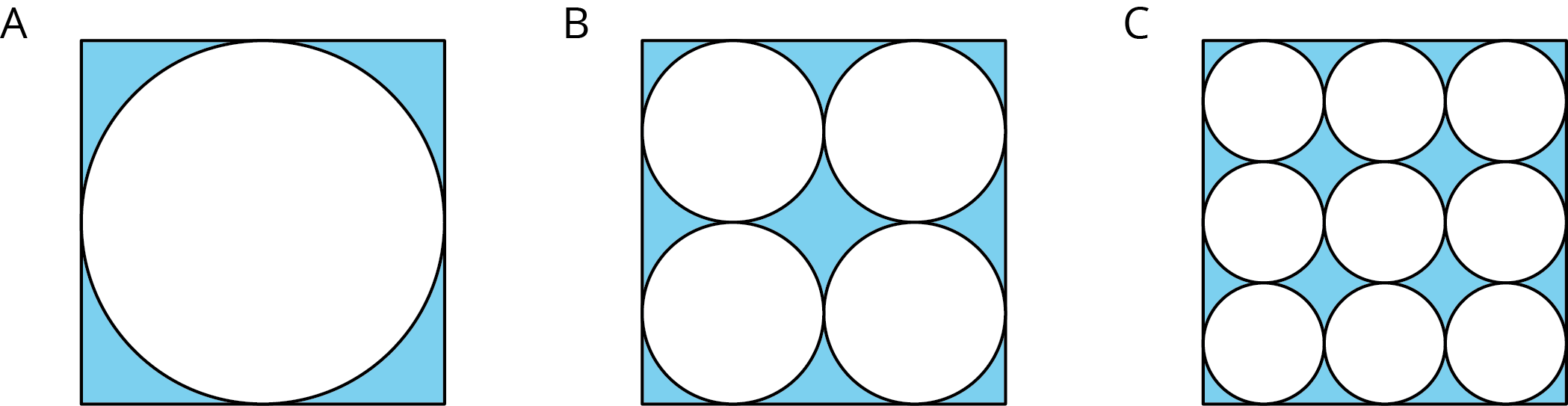
    Three equal sized figures labeled A B and C. Figure A is a square with a circle inside of it where the circle touches the midpoint of each side of the square. The regions outside of the circle are shaded blue. Figure B is a square with four identical circles inside of it that do not overlap. The circles are arranged in two rows of two circles, are tangent to each other and tangent to the sides of the square. The area outside of the circles is shaded blue. Figure C is a square with nine identical circles inside of it that do not overlap. The circles are arranged in three rows of three circles, are tangent to each other and to the sides of the square. The area outside of the circles is shaded blue.
  2. Each square in Figures D and E has a side length of 1 unit. Compare the area of the two figures. Which figure has more area? How much more? Explain or show your reasoning.
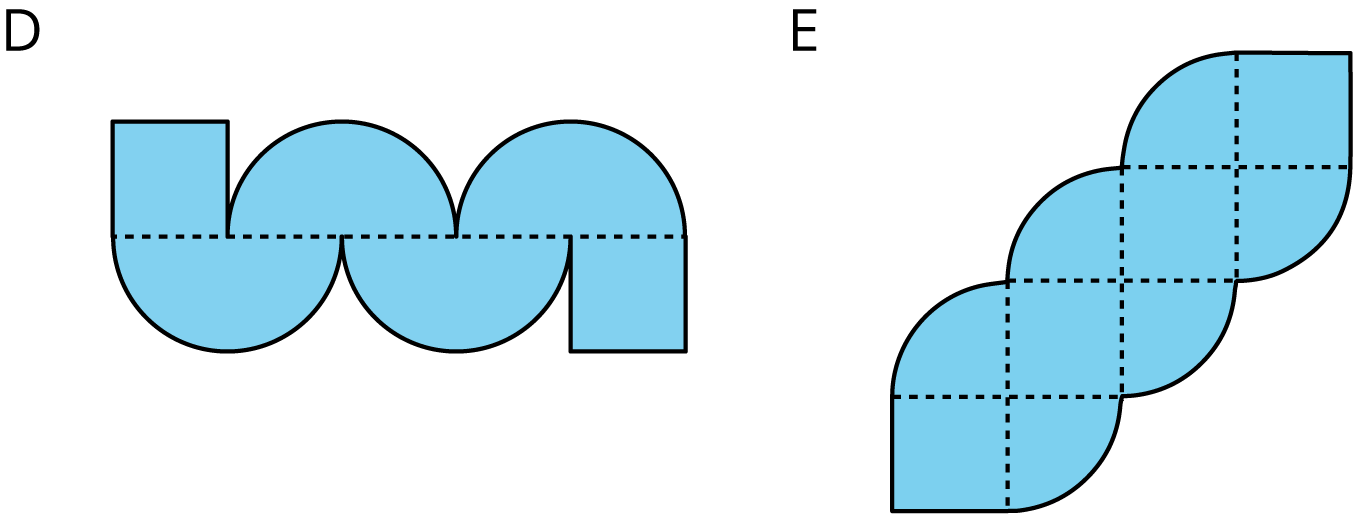
    Two figures, labeled D and E. Figure D is composed of one square and two semi circles on top, and two bottom halves of circles and one square on the bottom. The top and bottom are divided by a horizontal dashed line. Fiqure E is composed of 4 squares and 6 quarter circles. The 4 square are arranged diagonally, where the top right vertex of the first square is the same point as the bottom left vertex of the second square, the top right vertex of the second square is the same point as the bottom left vertex of the third square, and the top right vertex of the third square is the same point as the bottom left vertex of the fourth square. The corner circles align in between the sides of each square.

9.3: The Running Track Revisited

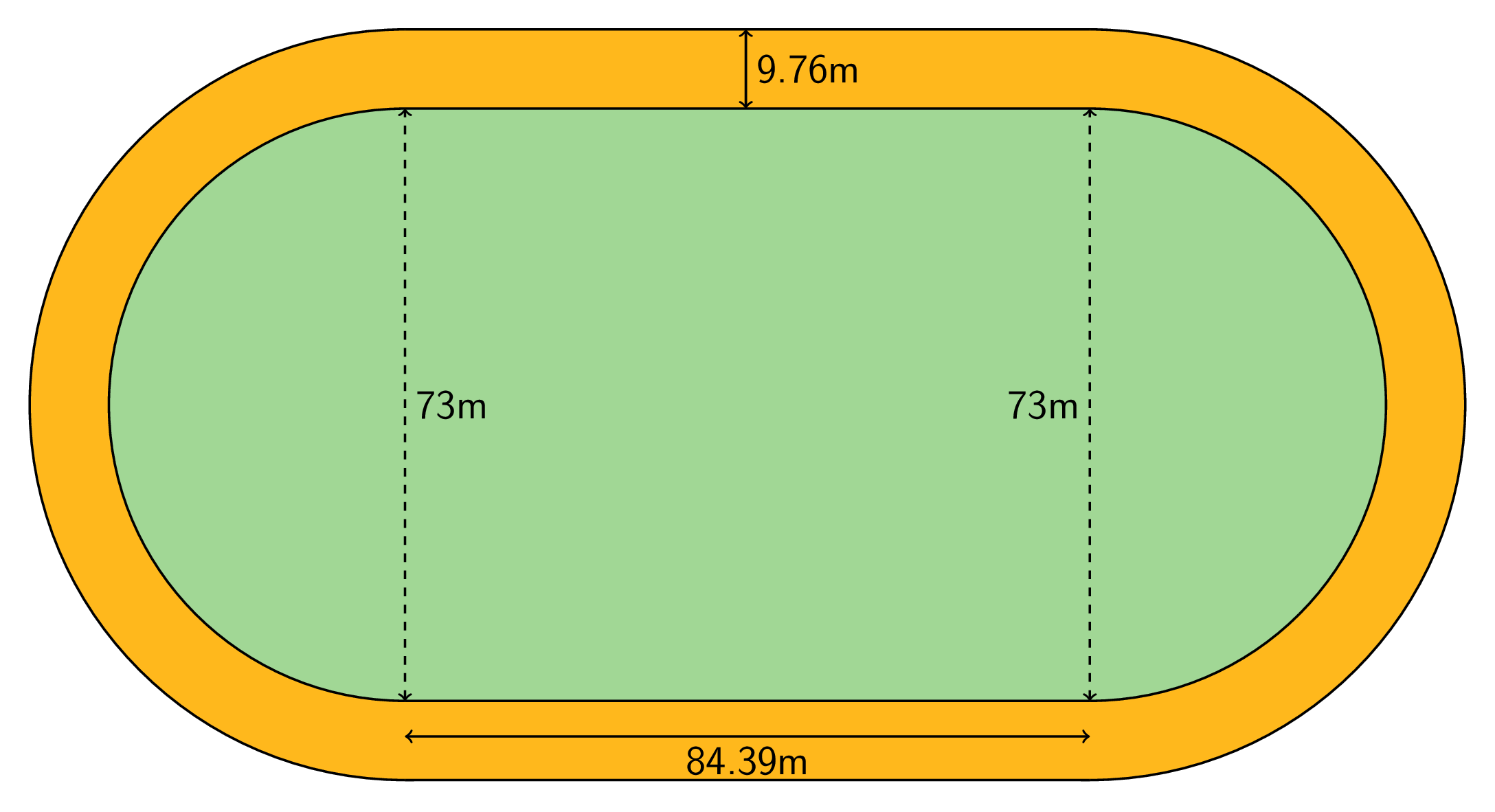
The field inside a running track is made up of a rectangle 84.39 m long and 73 m wide, together with a half-circle at each end. The running lanes are 9.76 m wide all the way around.

A picture of a field inside a running track. The field inside the track is composed of a rectangle, indicated by two dashed vertical lines labeled 73 meters and a horizontal length labeled 84 point 3 9 meters. There is a semi circle on each vertical side of the rectangle. The running track goes completely around the field and has a width of 9 point 7 6 meters.
What is the area of the running track that goes around the field? Explain or show your reasoning.

Summary

The relationship between $A$, the area of a circle, and $r$, its radius, is $A=\pi r^2$. We can use this to find the area of a circle if we know the radius. For example, if a circle has a radius of 10 cm, then the area is $\pi \boldcdot 10^2$ or $100\pi$ cm2. We can also use the formula to find the radius of a circle if we know the area. For example, if a circle has an area of $49 \pi$ m2 then its radius is 7 m and its diameter is 14 m. 

Sometimes instead of leaving $\pi$ in expressions for the area, a numerical approximation can be helpful. For the examples above, a circle of radius 10 cm has area about 314 cm2. In a similar way, a circle with area 154 m2 has radius about 7 m.

We can also figure out the area of a fraction of a circle. For example, the figure shows a circle divided into 3 pieces of equal area. The shaded part has an area of $\frac13 \pi r^2$.

A circle divided into three equal sections. From the center of the circle three line segments extend to a point on the circle. The line segment extending downward and to the right is labeled “r”. The upper left region of the circle is shaded.

Practice Problems ▶