7.1: Hanger Diagrams

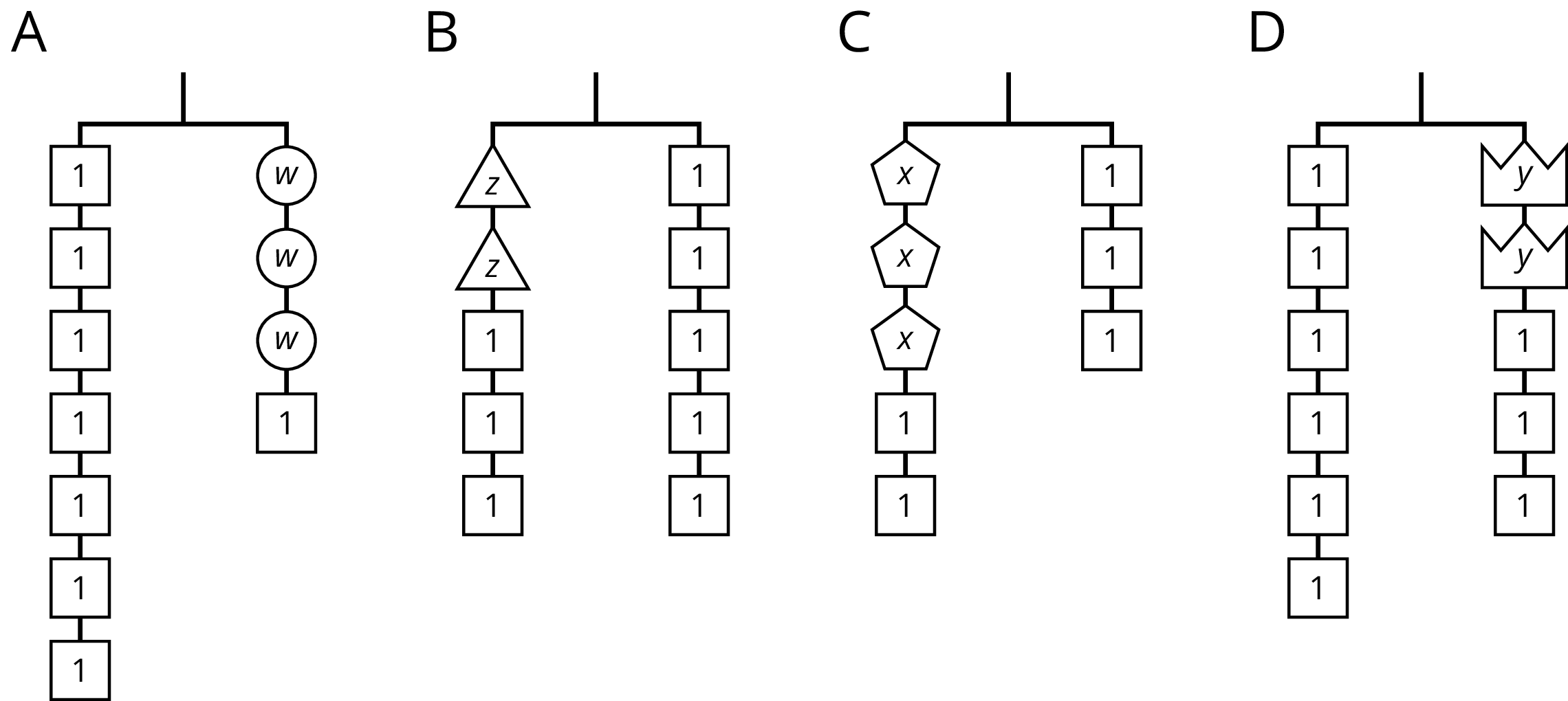
In the two diagrams, all the triangles weigh the same and all the squares weigh the same.
For each diagram, come up with . . .
- One thing that must be true
- One thing that could be true
- One thing that cannot possibly be true
Let’s see how a balanced hanger is like an equation and how moving its weights is like solving the equation.

In the two diagrams, all the triangles weigh the same and all the squares weigh the same.
For each diagram, come up with . . .
On each balanced hanger, figures with the same letter have the same weight.
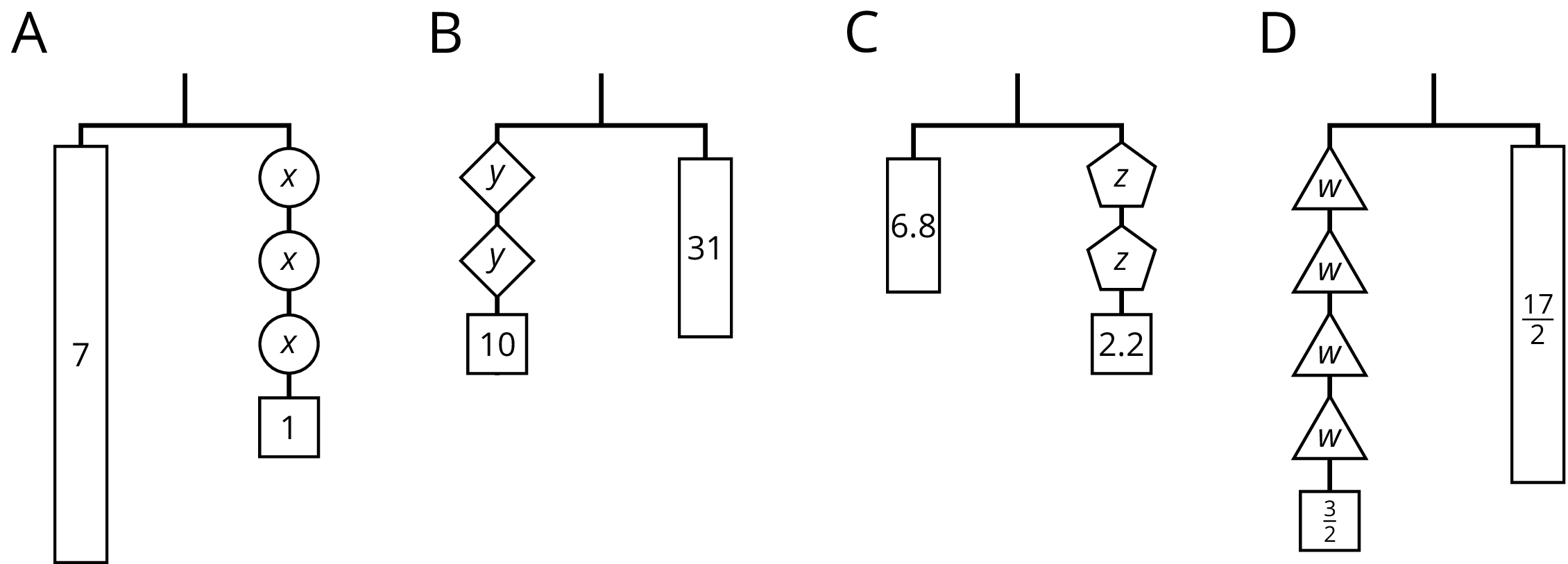
Here are some balanced hangers where each piece is labeled with its weight. For each diagram:
When you have the time, visit the site https://solveme.edc.org/Mobiles.html to solve some trickier puzzles that use hanger diagrams like the ones in this lesson. You can even build new ones. (If you want to do this during class, check with your teacher first!)
In this lesson, we worked with two ways to show that two amounts are equal: a balanced hanger and an equation. We can use a balanced hanger to think about steps to finding an unknown amount in an associated equation.
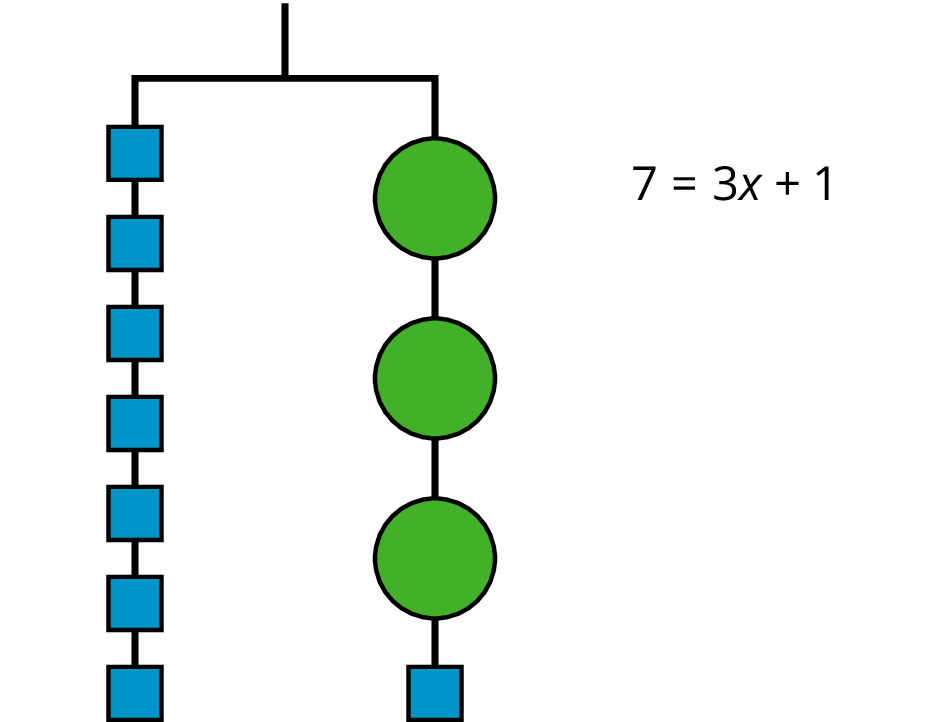
The hanger shows a total weight of 7 units on one side that is balanced with 3 equal, unknown weights and a 1-unit weight on the other. An equation that represents the relationship is $7=3x+1$.
We can remove a weight of 1 unit from each side and the hanger will stay balanced. This is the same as subtracting 1 from each side of the equation.
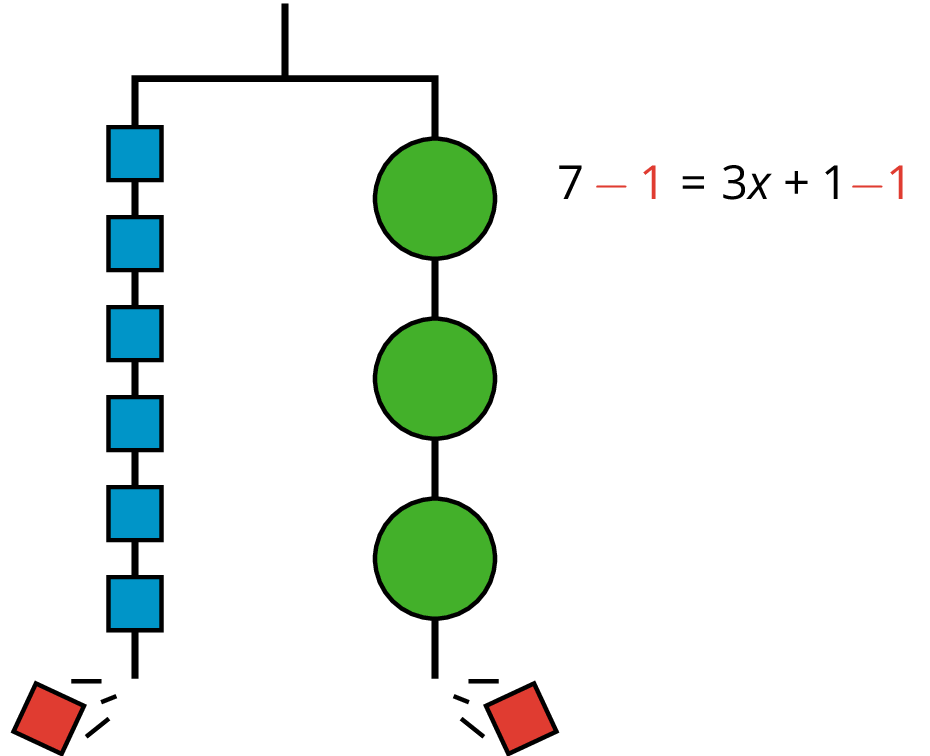
An equation for the new balanced hanger is $6=3x$.
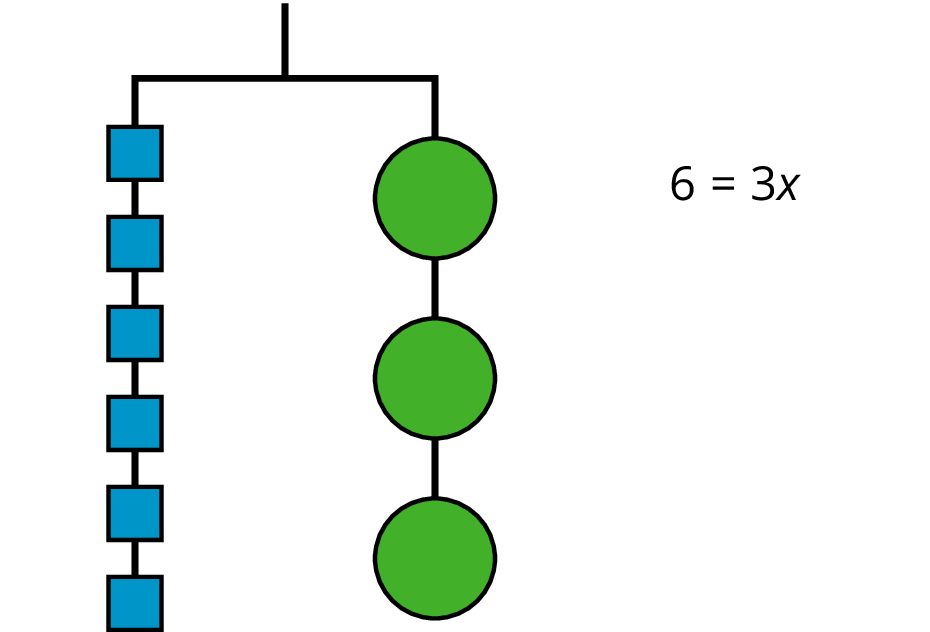
So the hanger will balance with $\frac13$ of the weight on each side: $\frac13 \boldcdot 6 = \frac13 \boldcdot 3x$.
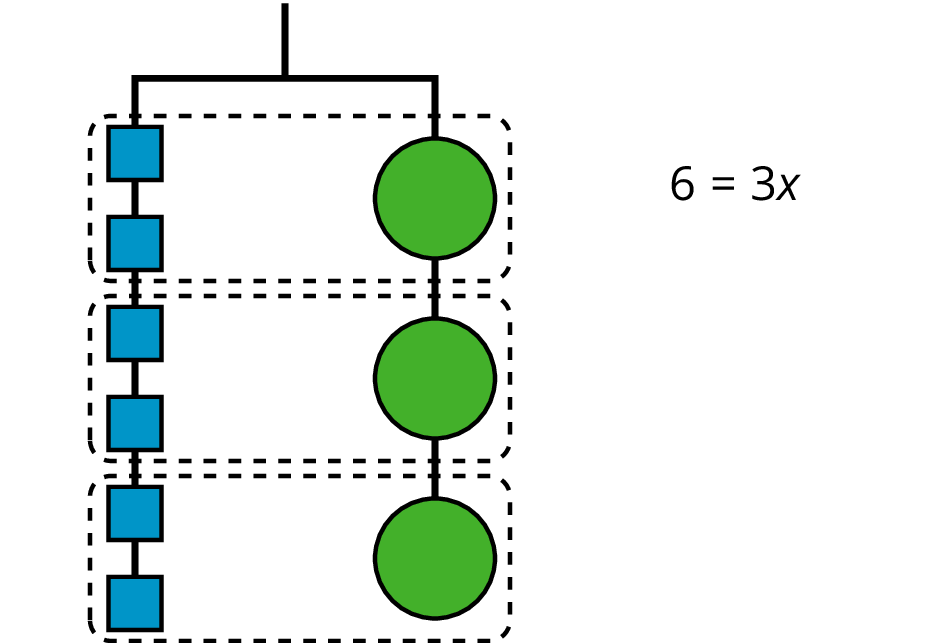
The two sides of the hanger balance with these weights: 6 1-unit weights on one side and 3 weights of unknown size on the other side.
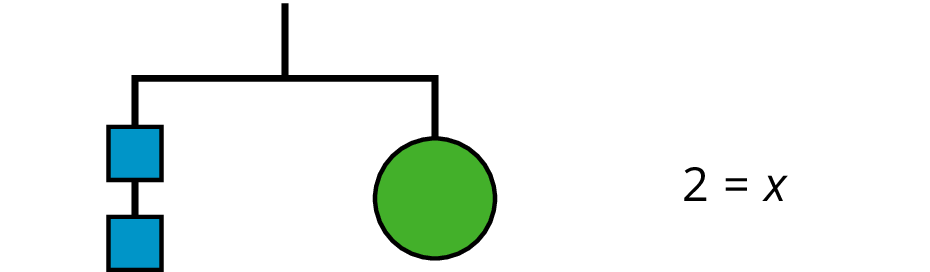
Here is a concise way to write the steps above:
\(\begin {align} 7&=3x+1 & \\ 6&=3x & \text{after subtracting 1 from each side} \\ 2 &= x & \text{after multiplying each side by } \tfrac13 \\ \end{align}\)