14.1: Multifaceted
Your teacher will show you a prism.
- What are some things you could measure about the object?
-
What units would you use for these measurements?
Let’s look at the surface area of prisms.
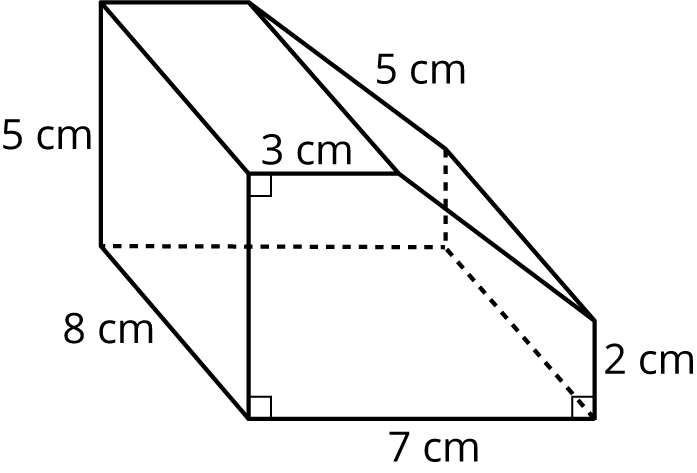
Your teacher will show you a prism.
Here is a picture of your teacher's prism:

Three students are trying to calculate the surface area of this prism.
Which method do you prefer? Why?
Between you and your partner, choose who will use each of these two methods to find the surface area of the prism.


In a deck of cards, each card measures 6 cm by 9 cm.
When stacked, the deck is 2 cm tall, as shown in the first photo. Find the volume of this deck of cards.
Then the cards are fanned out, as shown in the second picture. The distance from the rightmost point on the bottom card to the rightmost point on the top card is now 7 cm instead of 2 cm. Find the volume of the new stack.
To find the surface area of a three-dimensional figure whose faces are made up of polygons, we can find the area of each face, and add them up!
Sometimes there are ways to simplify our work. For example, all of the faces of a cube with side length $s$ are the same. We can find the area of one face, and multiply by 6. Since the area of one face of a cube is $s^2$, the surface area of a cube is $6s^2$.
We can use this technique to make it faster to find the surface area of any figure that has faces that are the same.
For prisms, there is another way. We can treat the prism as having three parts: two identical bases, and one long rectangle that has been taped along the edges of the bases. The rectangle has the same height as the prism, and its width is the perimeter of the base. To find the surface area, add the area of this rectangle to the areas of the two bases.