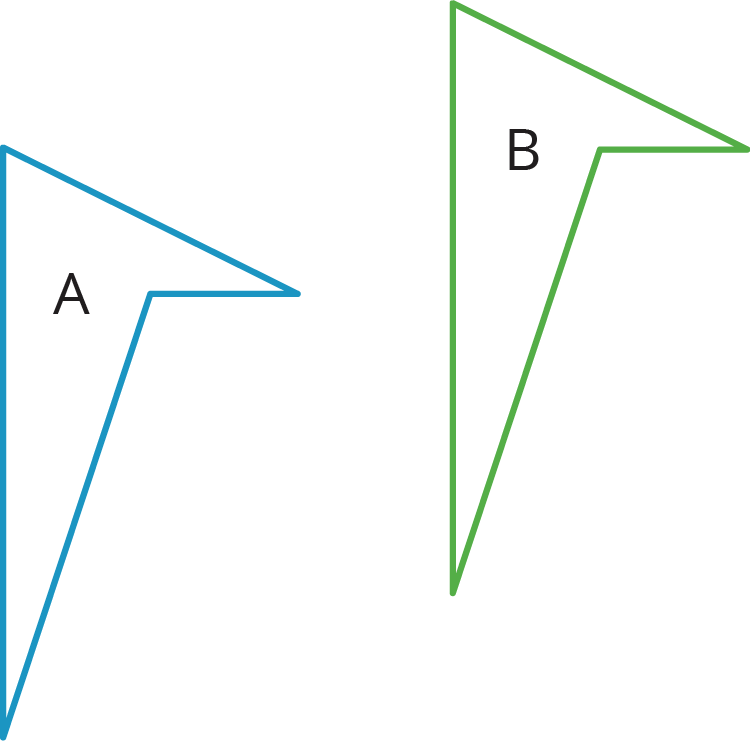
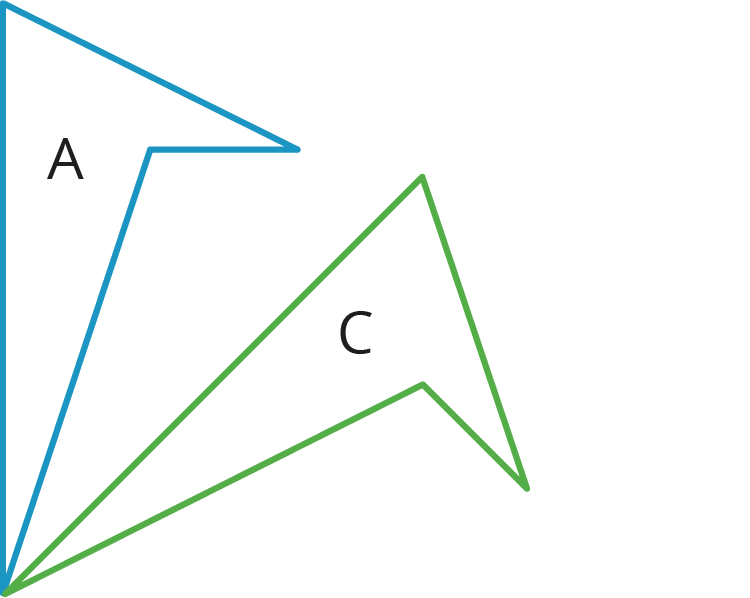
1.1: Which One Doesn’t Belong: Diagrams
Which one doesn’t belong?
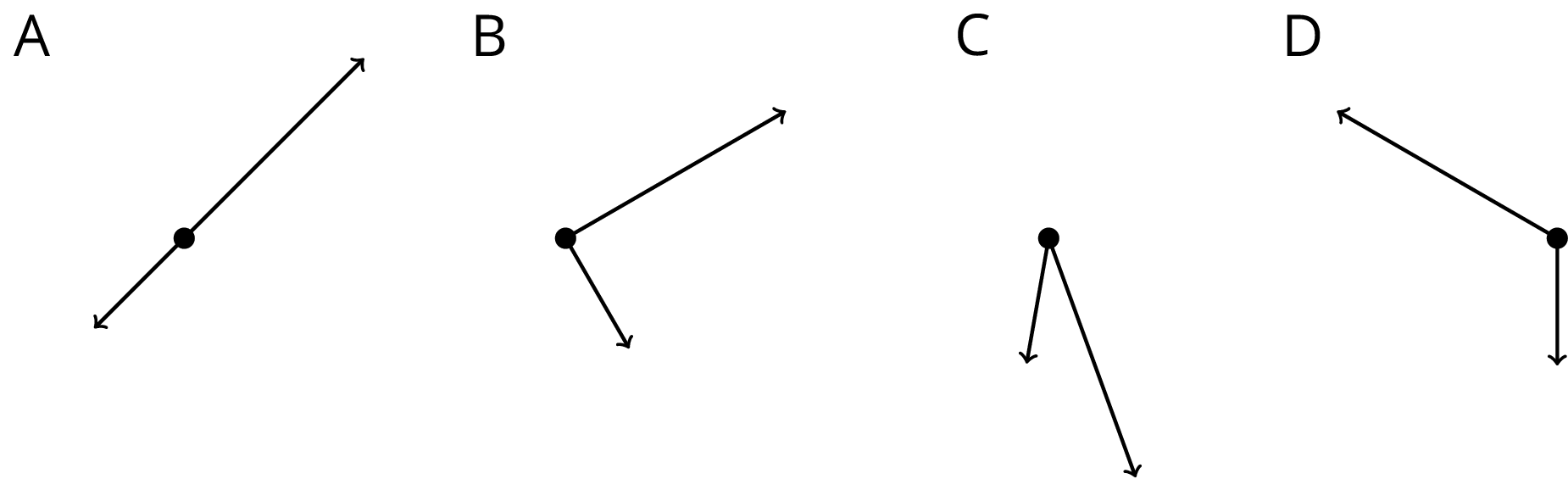
Let’s describe ways figures can move in the plane.
Which one doesn’t belong?

Your teacher will give you three pictures. Each shows a different set of dance moves.
Arrange the three pictures so one of you can see them right way up. Choose who will start the game.
The starting player chooses one of the three applets below and describes the dance to the other player.
The other player identifies which dance is being talked about: A, B, or C.
After one round, trade roles. When you have described all three dances, come to an agreement on the words you use to describe the moves in each dance.
With your partner, write a description of the moves in each dance.
Dance A:
Dance B:
Dance C:
We could think of each dance as a new dance by running it in reverse, starting in the 6th frame and working backwards to the first.
Pick a dance and describe in words one of these reversed dances.
How do the directions for running your dance in the forward direction and the reverse direction compare?
Here are two ways for changing the position of a figure in a plane without changing its shape or size: