Lesson 8: Rotation Patterns

Let’s rotate figures in a plane.

8.1: Building a Quadrilateral

Here is a right isosceles triangle:

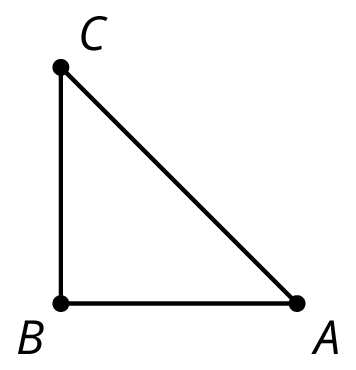
Right isosceles triangle A B C has horizonatl side A B with point A to the right of B, and has vertical side B C with point C directly above point B.
  1. Rotate triangle $ABC$ 90 degrees clockwise around $B$. 
  2. Rotate triangle $ABC$ 180 degrees clockwise round $B$.
  3. Rotate triangle $ABC$ 270 degrees clockwise around $B$.
  4. What would it look like when you rotate the four triangles 90 degrees clockwise around $B$? 180 degrees? 270 degrees clockwise?

8.2: Rotating a Segment

Create a segment $AB$ and a point $C$ that is not on segment $AB$.

GeoGebra Applet YF2EDCTt

  1. Rotate segment $AB$ $180^\circ$ around point $B$. 

  2. Rotate segment $AB$ $180^\circ$ around point $C$. 

Construct the midpoint of segment $AB$ with the Midpoint tool. 

  1. Rotate segment $AB$ $180^\circ$ around its midpoint. What is the image of A?

  2. What happens when you rotate a segment $180^\circ$?

8.3: A Pattern of Four Triangles

Here is a diagram built with three different rigid transformations of triangle $ABC$.

Use the applet to answer the questions. It may be helpful to reset the image after each question.

GeoGebra Applet Ccv3FucS

  1. Describe a rigid transformation that takes triangle $ABC$ to triangle $CDE$.
  2. Describe a rigid transformation that takes triangle $ABC$ to triangle $EFG$.
  3. Describe a rigid transformation that takes triangle $ABC$ to triangle $GHA$.
  4. Do segments $AC$, $CE$, $EG$, and $GA$ all have the same length? Explain your reasoning.

Summary

When we apply a 180-degree rotation to a line segment, there are several possible outcomes:

  • The segment maps to itself (if the center of rotation is the midpoint of the segment).
  • The image of the segment overlaps with the segment and lies on the same line (if the center of rotation is a point on the segment).
  • The image of the segment does not overlap with the segment (if the center of rotation is not on the segment).

We can also build patterns by rotating a shape. For example, triangle $ABC$ shown here has $m(\angle A) = 60$. If we rotate triangle $ABC$ 60 degrees, 120 degrees, 180 degrees, 240 degrees, and 300 degrees clockwise, we can build a hexagon.

Six identical equilateral triangles are drawn such that each triangle is aligned to another triangle created a hexagon. One of the triangle is labeled A B C and all 6 triangles meet at the common point of A.

Practice Problems ▶