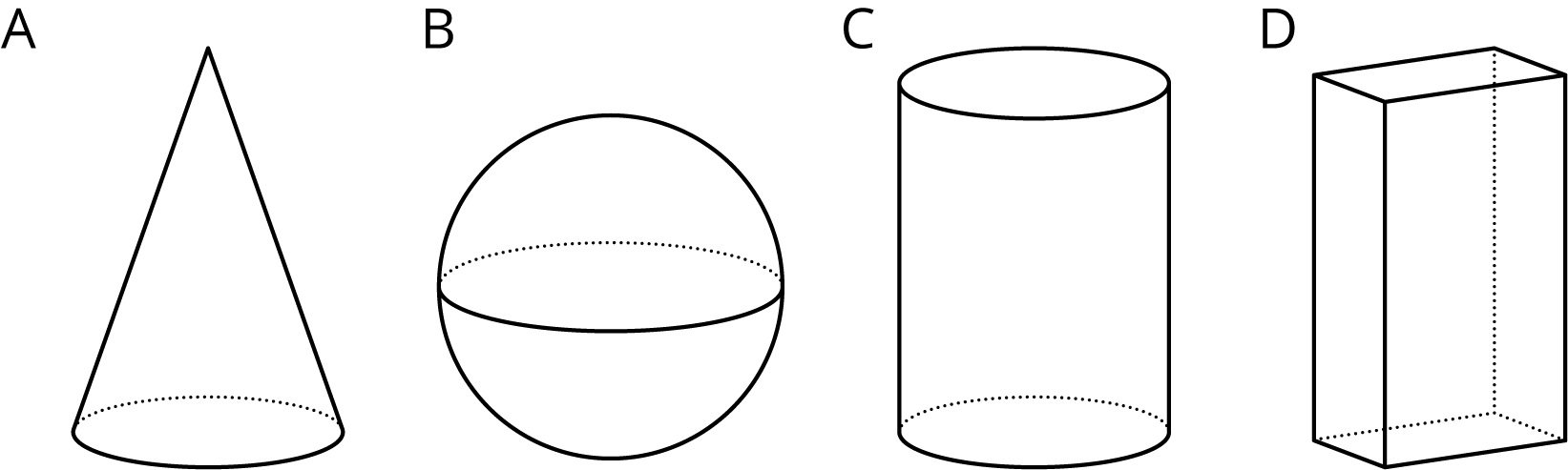
11.1: Which One Doesn’t Belong: Solids
These are drawings of three-dimensional objects. Which one doesn’t belong? Explain your reasoning.
Let’s fill containers with water.
These are drawings of three-dimensional objects. Which one doesn’t belong? Explain your reasoning.

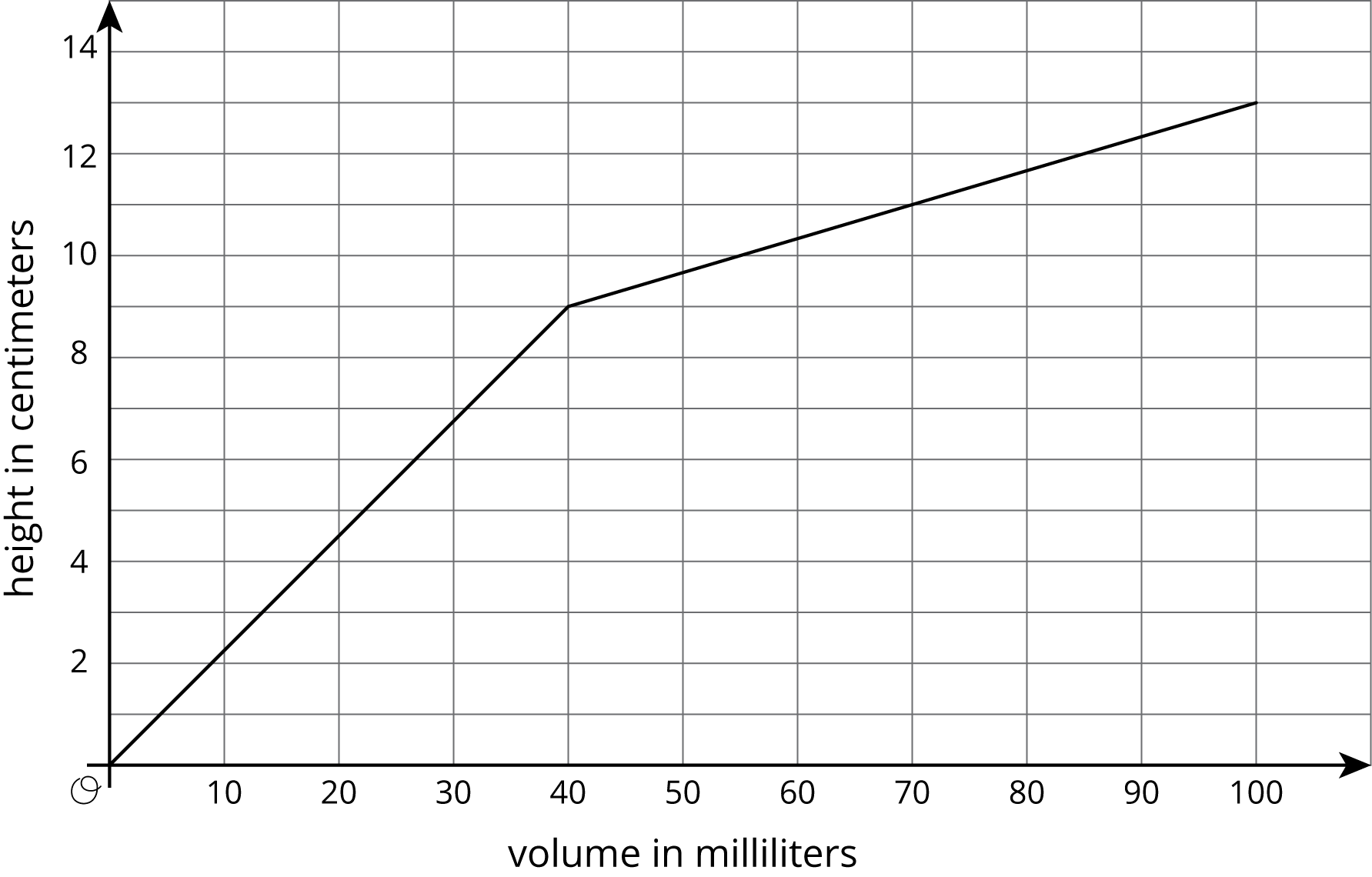
Use the applet to investigate the height of water in the cylinder as a function of the water volume.
Before you get started, make a prediction about the shape of the graph.
Check Reset and set the radius and height of the graduated cylinder to values you choose.
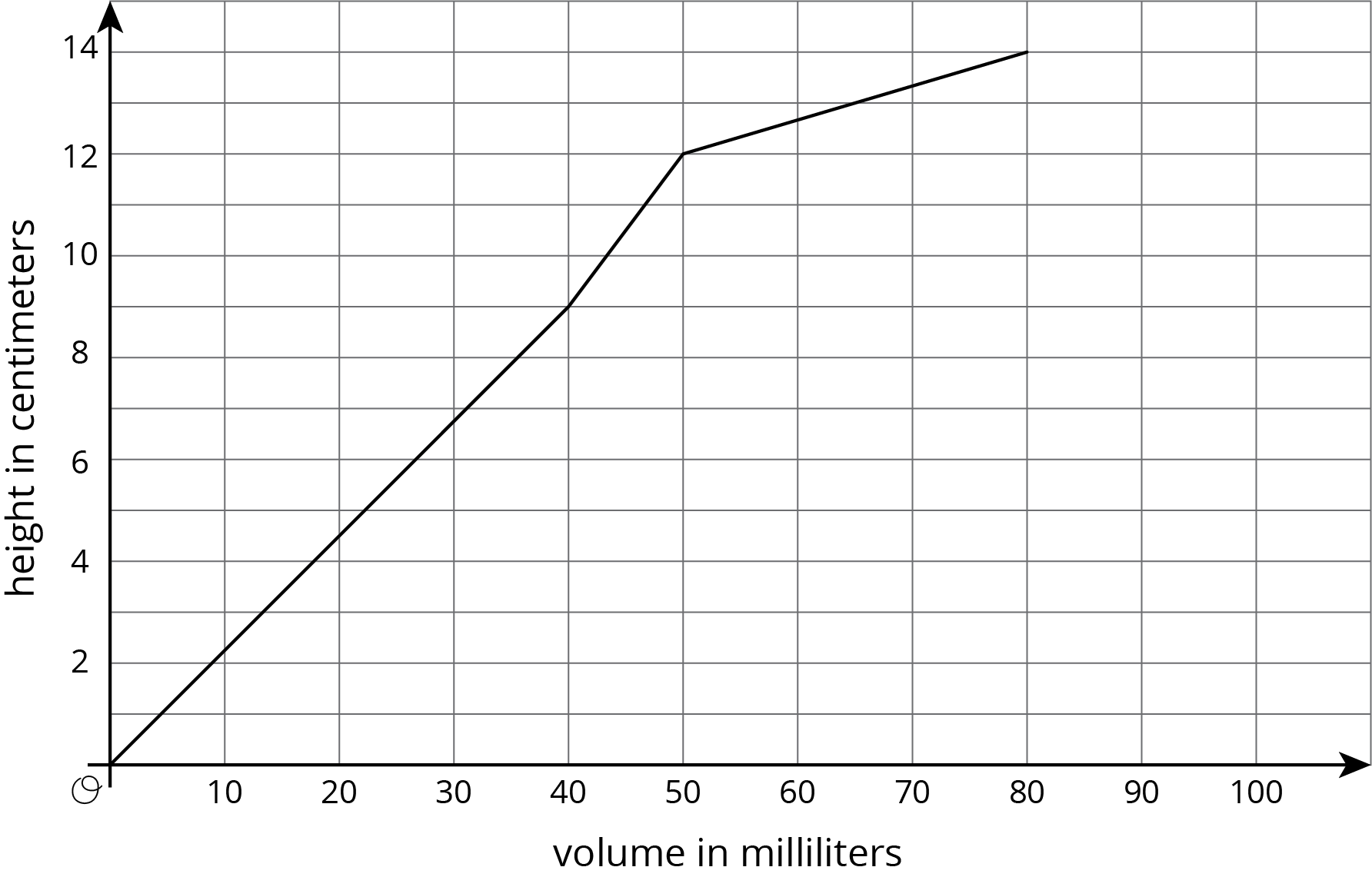
The graph shows the height vs. volume function of an unknown container. What shape could this container have? Explain how you know and draw a possible container.
When filling a shape like a cylinder with water, we can see how the dimensions of the cylinder affect things like the changing height of the water. For example, let's say we have two cylinders, $D$ and $E$, with the same height, but $D$ has a radius of 3 cm and $E$ has a radius of 6 cm.
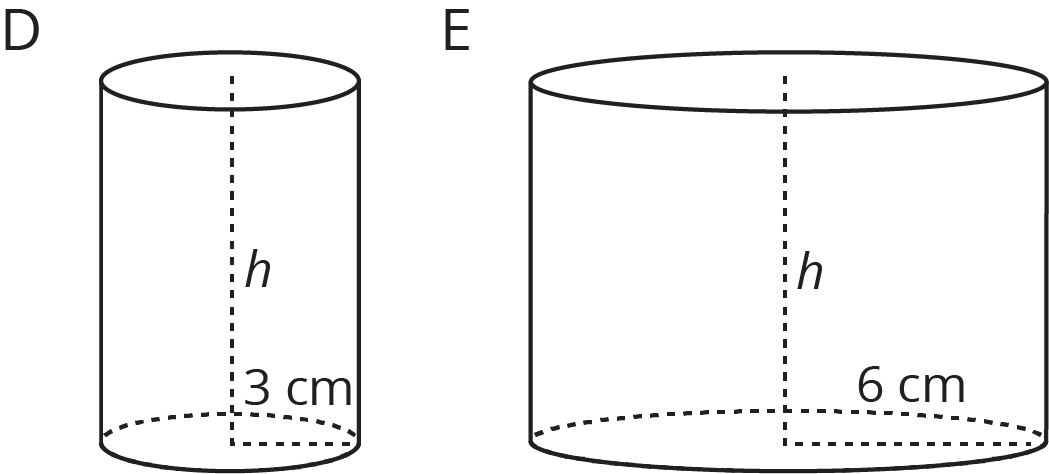
If we pour water into both cylinders at the same rate, the height of water in $D$ will increase faster than the height of water in $E$ due to its smaller radius. This means that if we made graphs of the height of water as a function of the volume of water for each cylinder, we would have two lines and the slope of the line for cylinder $D$ would be greater than the slope of the line for cylinder $E$.