3.1: A Square’s Area
Fill in the table of input-output pairs for the given rule. Write an algebraic expression for the rule in the box in the diagram.
| input | output | |
|---|---|---|
| row 1 | 8 | |
| row 2 | 2.2 | |
| row 3 | $12\frac14$ | |
| row 4 | $s$ |
Lesson 3: Equations for Functions
Let’s find outputs from equations.
3.2: Diagrams, Equations, and Descriptions
Record your answers to these questions in the table provided:
- Match each of these descriptions with a diagram:
- the circumference, $C$, of a circle with radius, $r$
- the distance in miles, $d$, that you would travel in $t$ hours if you drive at 60 miles per hour
- the output when you triple the input and subtract 4
- the volume of a cube, $v$ given its edge length, $s$
- Write an equation for each description that expresses the output as a function of the input.
- Find the output when the input is 5 for each equation.
- Name the independent and dependent variables of each equation.
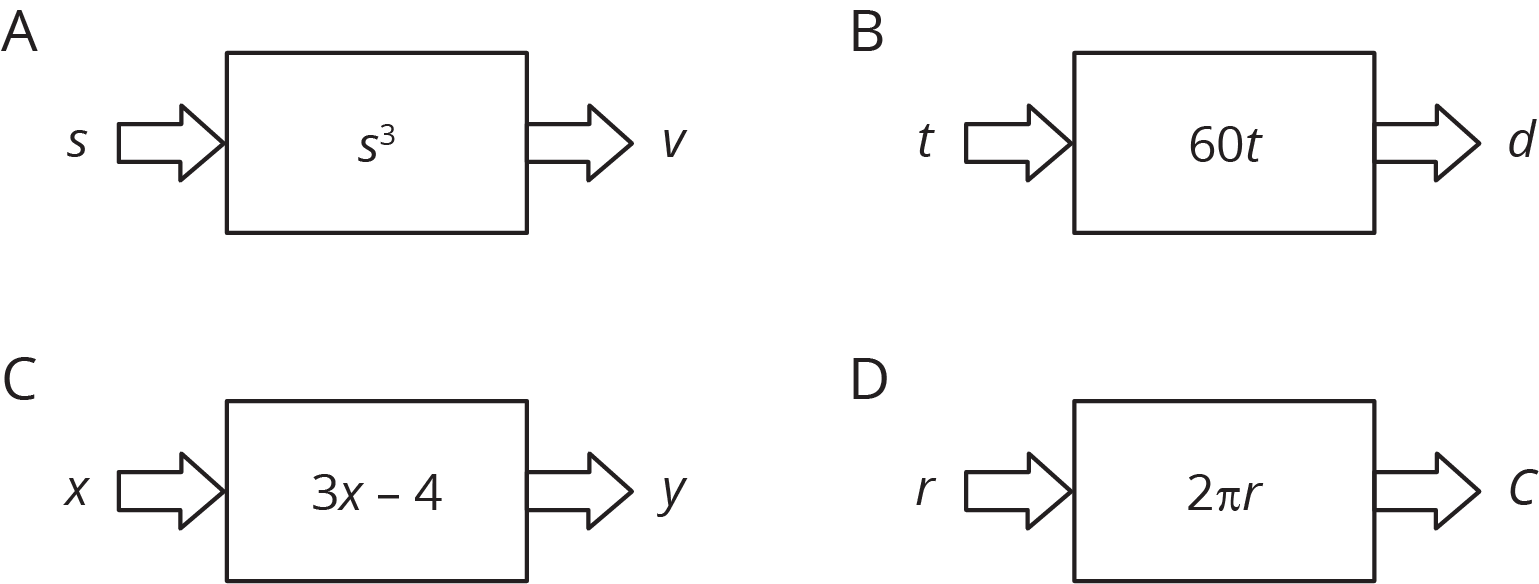
| description | a | b | c | d |
|---|---|---|---|---|
| diagram | |
|||
| equation | |
|||
| input = 5 output = ? |
||||
| independent variable |
||||
| dependent variable |
Choose a 3-digit number as an input and apply the following rule to it, one step at a time:
- Multiply your number by 7.
- Add one to the result.
- Multiply the result by 11.
- Subtract 5 from the result.
- Multiply the result by 13
- Subtract 78 from the result to get the output.
Can you describe a simpler way to describe this rule? Why does this work?
3.3: Dimes and Quarters
Jada had some dimes and quarters that had a total value of \$12.50. The relationship between the number of dimes, $d$, and the number of quarters, $q$, can be expressed by the equation $0.1d + 0.25q = 12.5$.
- If Jada has 4 quarters, how many dimes does she have?
- If Jada has 10 quarters, how many dimes does she have?
- Is the number of dimes a function of the number of quarters? If yes, write a rule (that starts with $d = $...) that you can use to determine the output, $d$, from a given input, $q$. If no, explain why not.
- If Jada has 25 dimes, how many quarters does she have?
- If Jada has 30 dimes, how many quarters does she have?
- Is the number of quarters a function of the number of dimes? If yes, write a rule (that starts with $q=$...) that you can use to determine the output, $q$, from a given input, $d$. If no, explain why not.
Summary
We can sometimes represent functions with equations. For example, the area, $A$, of a circle is a function of the radius, $r$, and we can express this with an equation: $$A=\pi r^2$$
We can also draw a diagram to represent this function:
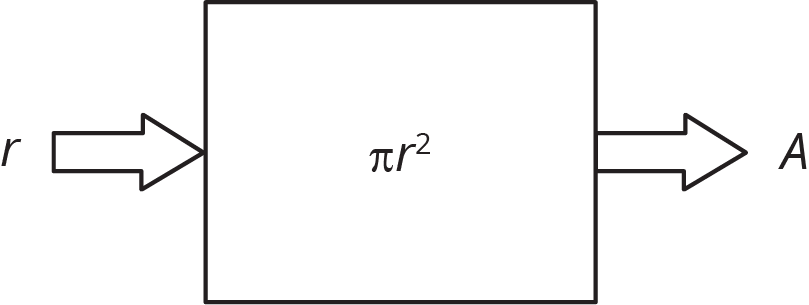
In this case, we think of the radius, $r$, as the input, and the area of the circle, $A$, as the output. For example, if the input is a radius of 10 cm, then the output is an area of $100\pi$ cm2, or about 314 square cm. Because this is a function, we can find the area, $A$, for any given radius, $r$.
Since it is the input, we say that $r$ is the independent variable and, as the output, $A$ is the dependent variable.
Sometimes when we have an equation we get to choose which variable is the independent variable. For example, if we know that
$$10A-4B=120$$
then we can think of $A$ as a function of $B$ and write
$$A=0.4B+12$$
or we can think of $B$ as a function of $A$ and write
$$B=2.5A-30$$
Practice Problems ▶
Glossary
-
independent variable
independent variable
A variable representing the input of a function.
-
dependent variable
dependent variable
A variable representing the output of a function.