19.1: Notice and Wonder: Two Shapes
Here are two shapes.
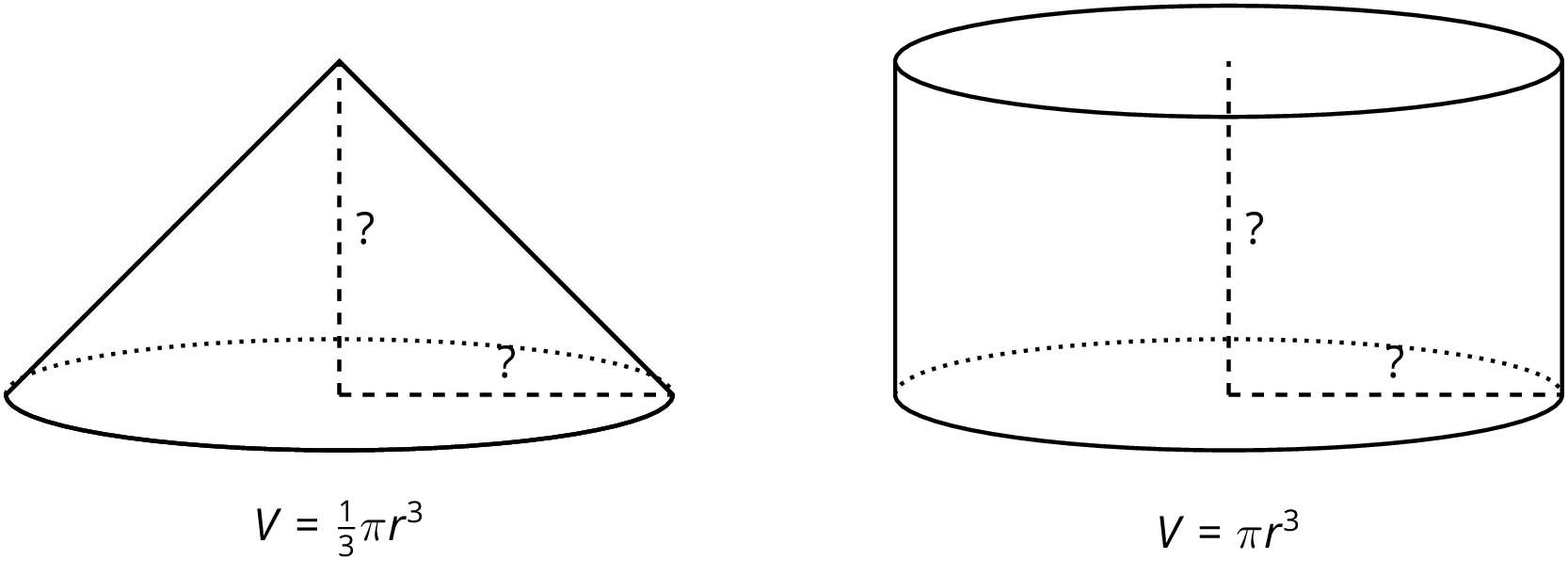
What do you notice? What do you wonder?
Let’s estimate volume of hemispheres with figures we know.
Here are two shapes.

What do you notice? What do you wonder?
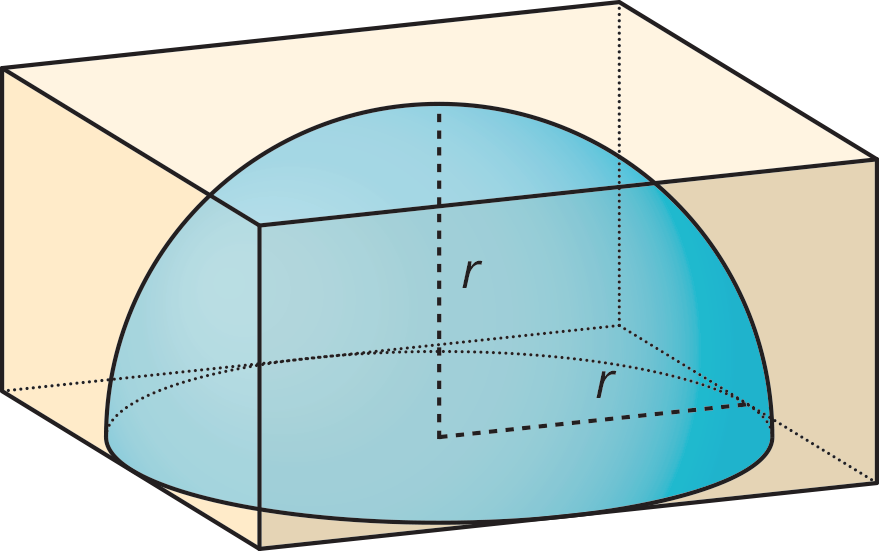

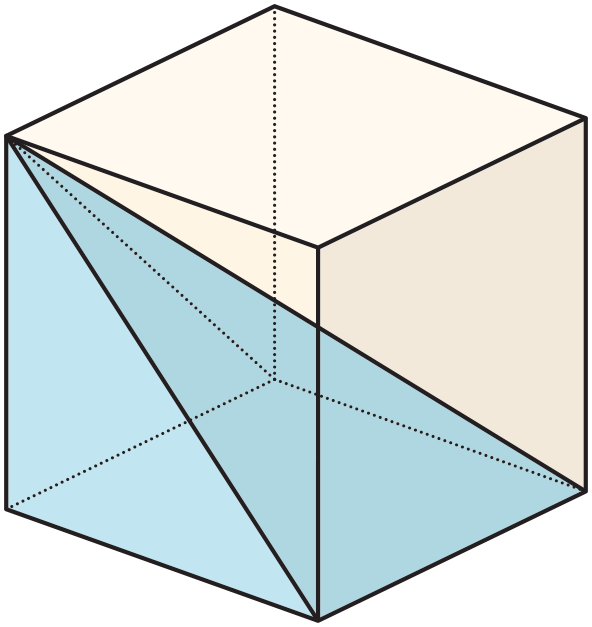
Estimate what fraction of the volume of the cube is occupied by the pyramid that shares the base and a top vertex with the cube, as in the figure.
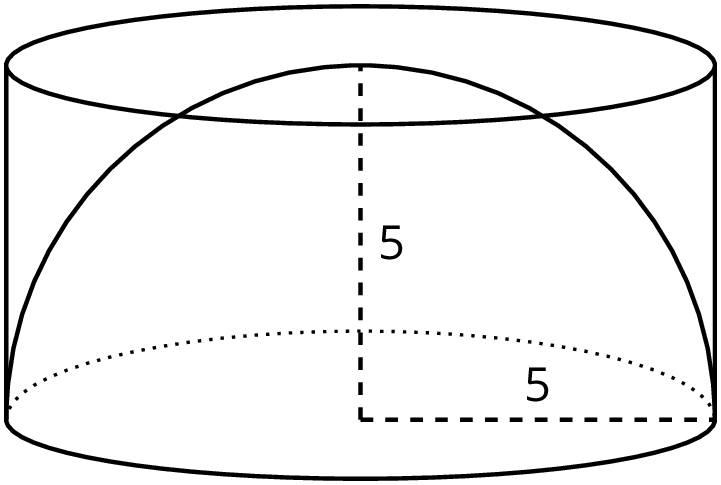
We can estimate the volume of a hemisphere by comparing it to other shapes for which we know the volume. For example, a hemisphere of radius 1 unit fits inside a cylinder with a radius of 1 unit and height of 1 unit.
Since the hemisphere is inside the cylinder, it must have a smaller volume than the cylinder making the cylinder's volume a reasonable over-estimate for the volume of the hemisphere.
The volume of this particular cylinder is about 3.14 units3 since \pi(1)^2(1)=\pi, so we know the volume of the hemisphere is less than 3.14 cubic units.
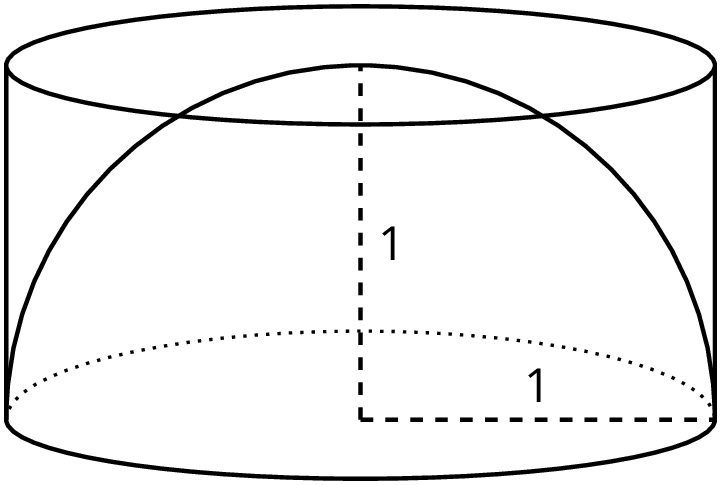
Using similar logic, a cone of radius 1 unit and height 1 unit fits inside of the hemisphere of radius 1 unit.
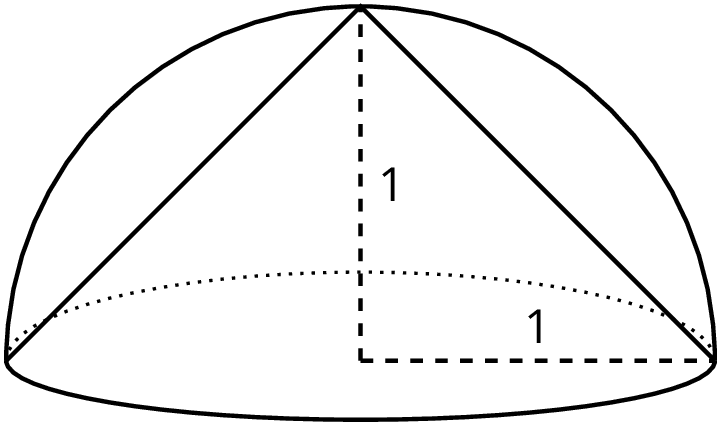
Since the cone is inside the hemisphere, the cone must have a smaller volume than the hemisphere making the cone's volume a reasonable under-estimate for the volume of the hemisphere.
The volume of this particular cone is about 1.05 units3 since \frac13 \pi(1)^2(1)=\frac13 \pi \approx 1.05, so we know the volume of the hemisphere is more than 1.05 cubic units.
Averaging the volumes of the cylinder and the cone, we can estimate the volume of the hemisphere to be about 2.10 units3 since \frac {3.14+1.05}2 \approx 2.10. And, since a hemisphere is half of a sphere, we can also estimate that a sphere with radius of 1 would be double this volume, or about 4.20 units3.