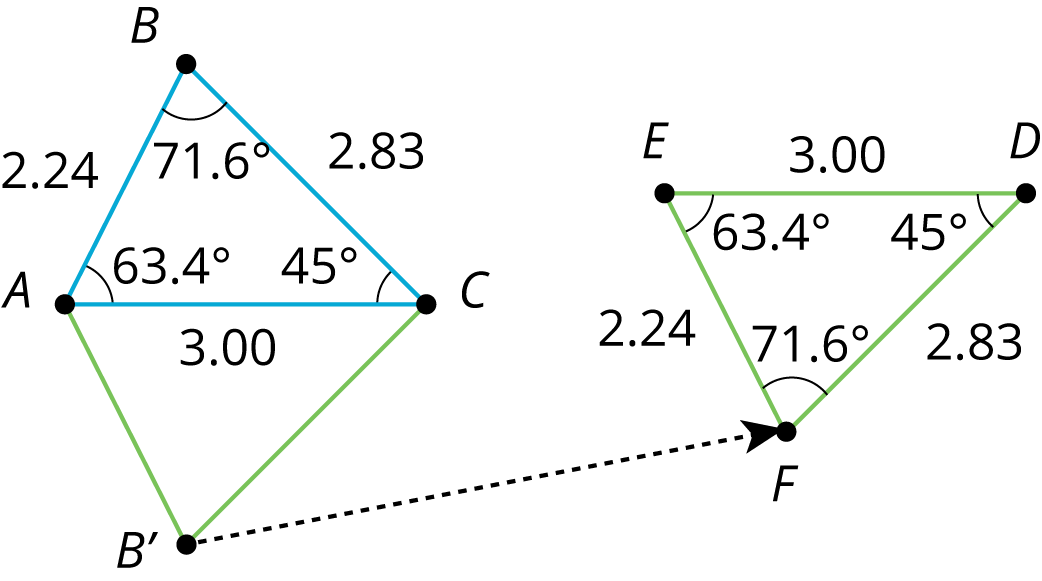The transformations we’ve learned about so far, translations, rotations, reflections, and sequences of these motions, are all examples of rigid transformations. A rigid transformation is a move that doesn’t change measurements on any figure.
Earlier, we learned that a figure and its image have corresponding points. With a rigid transformation, figures like polygons also have corresponding sides and corresponding angles. These corresponding parts have the same measurements.
For example, triangle $EFD$ was made by reflecting triangle $ABC$ across a horizontal line, then translating. Corresponding sides have the same lengths, and corresponding angles have the same measures.
| |
measurements in triangle $ABC$ |
corresponding measurements in image $EFD$ |
| row 1 |
$AB = 2.24$ |
$EF = 2.24$ |
| row 2 |
$BC = 2.83$ |
$FD = 2.83$ |
| row 3 |
$CA = 3.00$ |
$DE = 3.00$ |
| row 4 |
$m\angle ABC = 71.6^\circ$ |
$m\angle EFD= 71.6^\circ$ |
| row 5 |
$m\angle BCA = 45.0^\circ$ |
$m\angle FDE= 45.0^\circ$ |
| row 6 |
$m\angle CAB = 63.4^\circ$ |
$m\angle DEF= 63.4^\circ$ |