Lesson 1: Projecting and Scaling

Let’s explore scaling.

1.1: Number Talk: Remembering Fraction Division

Find each quotient. Write your answer as a fraction or a mixed number.

$6\frac14 \div 2$

$10\frac17 \div 5$

$8\frac12 \div 11$

1.2: Sorting Rectangles

Rectangles were made by cutting an $8\frac12$-inch by 11-inch piece of paper in half, in half again, and so on, as illustrated in the diagram. Find the lengths of each rectangle and enter them in the appropriate table.

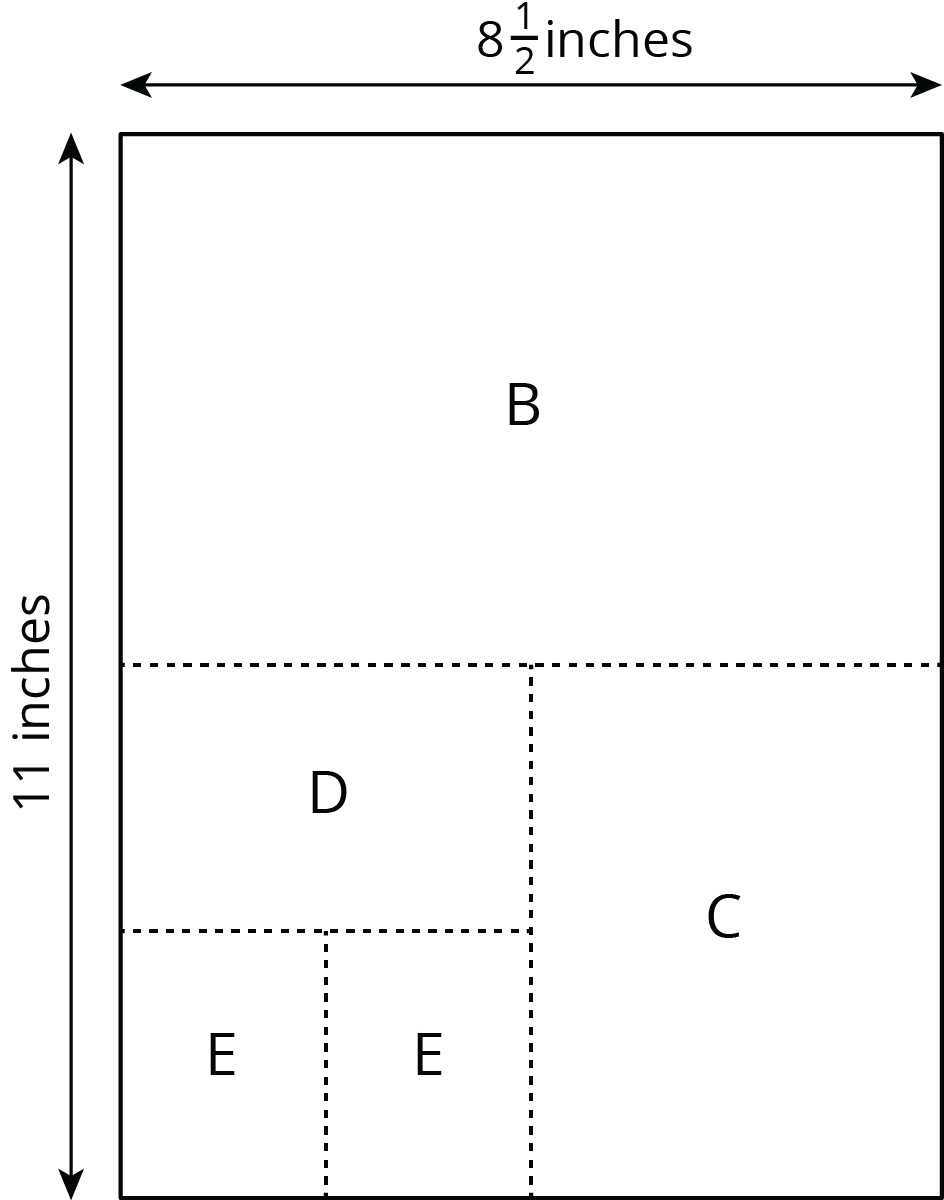
  1. Some of the rectangles are scaled copies of the full sheet of paper (Rectangle A). Enter the measurements of those rectangles in the table.
      rectangle length of short side (inches) length of long side (inches)
    row 1 A $8 \frac{1}{2}$ 11
    row 2      
    row 3      
    row 4      
  2. Some of the rectangles are not scaled copies of the full sheet of paper. Enter the measurements of those rectangles in the table.
      rectangle length of short side (inches) length of long side (inches)
    row 1      
    row 2      
    row 3      
  3. Look at the measurements for the rectangles that are scaled copies of the full sheet of paper. What do you notice about the measurements of these rectangles? Look at the measurements for the rectangles that are not scaled copies of the full sheet. What do you notice about these measurements?
  4. Stack the rectangles that are scaled copies of the full sheet so that they all line up at a corner, as shown in the diagram. Do the same with the other set of rectangles. On each stack, draw a line from the bottom left corner to the top right corner of the biggest rectangle. What do you notice?
  5. Stack all of the rectangles from largest to smallest so that they all line up at a corner. Compare the lines that you drew. Can you tell, from the drawn lines, which set each rectangle came from?

1.3: Scaled Rectangles

Here is a picture of Rectangle R, which has been evenly divided into smaller rectangles. Two of the smaller rectangles are labeled B and C.

  1. Is $B$ a scaled copy of $R$? If so, what is the scale factor?
  2. Is $C$ a scaled copy of $B$? If so, what is the scale factor?
  3. Is $C$ a scaled copy of $R$? If so, what is the scale factor?
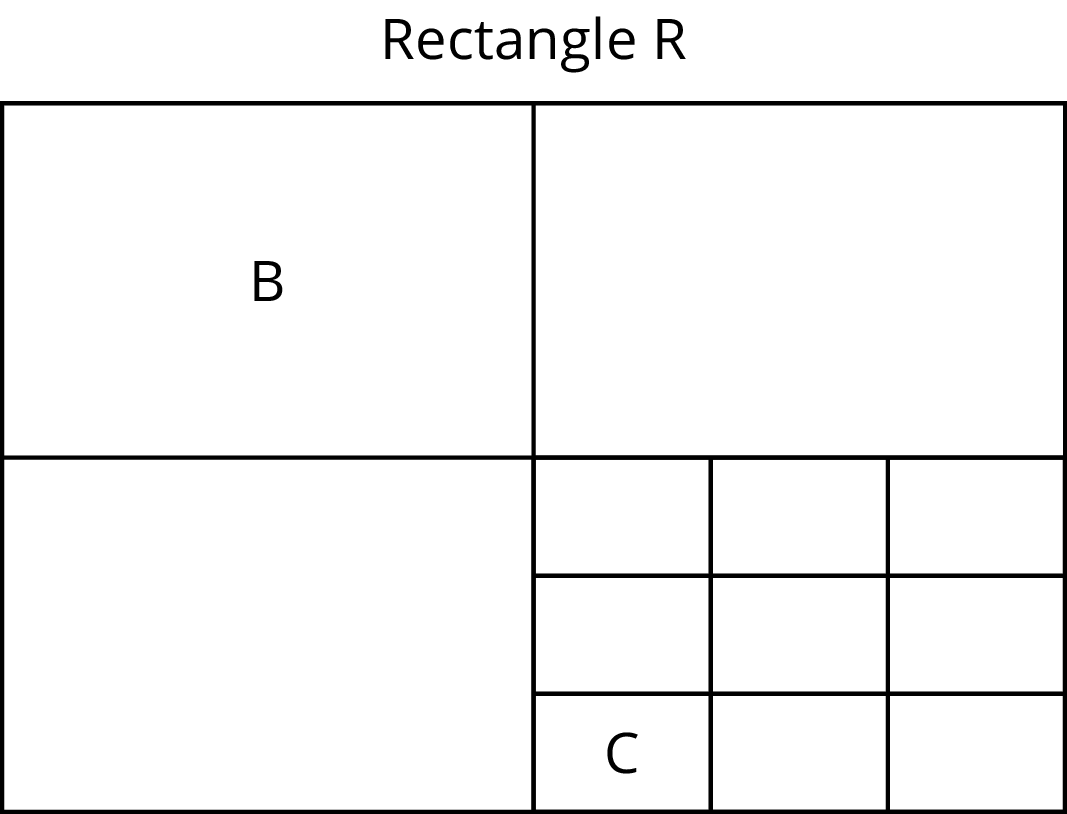
A rectangle labeled R is evenly divided into 4 equal sized smaller rectangles. The top right rectangle is labeled B. The bottom right rectangle, is further evenly divided into 9 equal sized smaller rectangle, in which one of those rectangles are labeled C.

Summary

Scaled copies of rectangles have an interesting property. Can you see what it is?

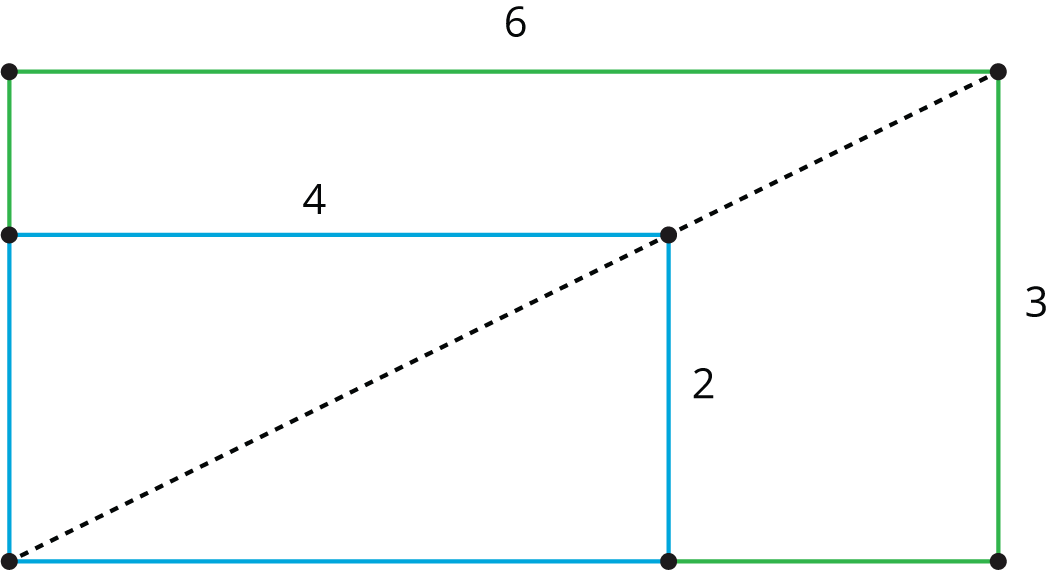
Here, the larger rectangle is a scaled copy of the smaller one (with a scale factor of $\frac{3}{2}$). Notice how the diagonal of the large rectangle contains the diagonal of the smaller rectangle. This is the case for any two scaled copies of a rectangle if we line them up as shown. If two rectangles are not scaled copies of one another, then the diagonals do not match up. In this unit, we will investigate how to make scaled copies of a figure.

Practice Problems ▶