3.1: Notice and Wonder: The Isometric Grid
What do you notice? What do you wonder?

Let’s transform some figures on grids.
What do you notice? What do you wonder?

Follow the directions below each statement to tell GeoGebra how you want the figure to move. It is important to notice that GeoGebra uses vectors to show translations. A vector is a quantity that has magnitude (size) and direction. It is usually represented by an arrow.
These applets are sensitive to clicks. Be sure to make one quick click, otherwise it may count a double-click.
After each example, click the reset button, and then move the slider over for the next question.
Translate triangle $ABC$ so that $C$ goes to $C’$.
Try your own translations, reflections, and rotations.
When a figure is on a grid, we can use the grid to describe a transformation. For example, here is a figure and an image of the figure after a move.
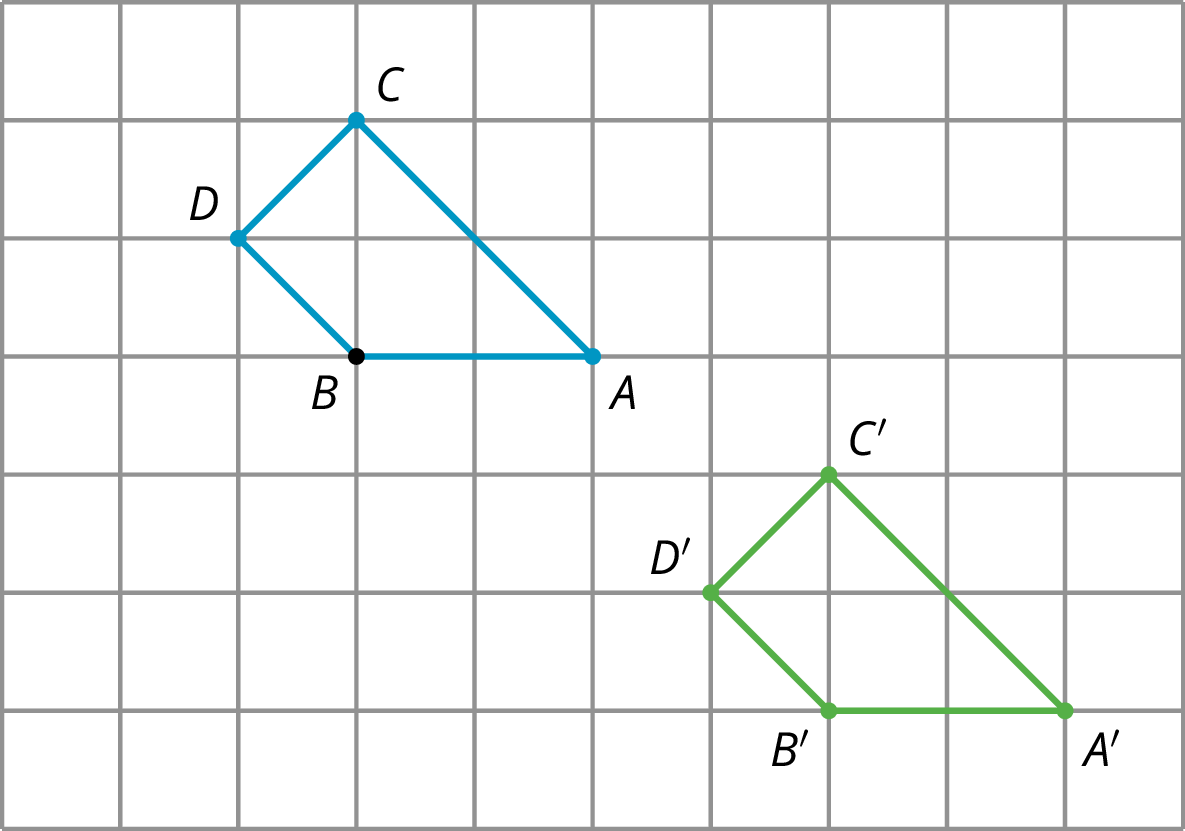
Quadrilateral $ABCD$ is translated 4 units to the right and 3 units down to the position of quadrilateral $A'B'C'D'$.
A second type of grid is called an isometric grid. The isometric grid is made up of equilateral triangles. The angles in the triangles all measure 60 degrees, making the isometric grid convenient for showing rotations of 60 degrees.

Here is quadrilateral $KLMN$ and its image $K'L'M'N'$ after a 60-degree counterclockwise rotation around a point $P$.