4.1: Reflection Quick Image
Here is an incomplete image. Your teacher will flash the completed image twice. Your job is to complete the image on your copy.
Let’s draw and describe translations, rotations, and reflections.
Here is an incomplete image. Your teacher will flash the completed image twice. Your job is to complete the image on your copy.
Your partner will describe the image of this triangle after a certain transformation. Sketch it here.
Here are some figures on an isometric grid. Explore the transformation tools in the tool bar. (Directions are below the applet if you need them.)
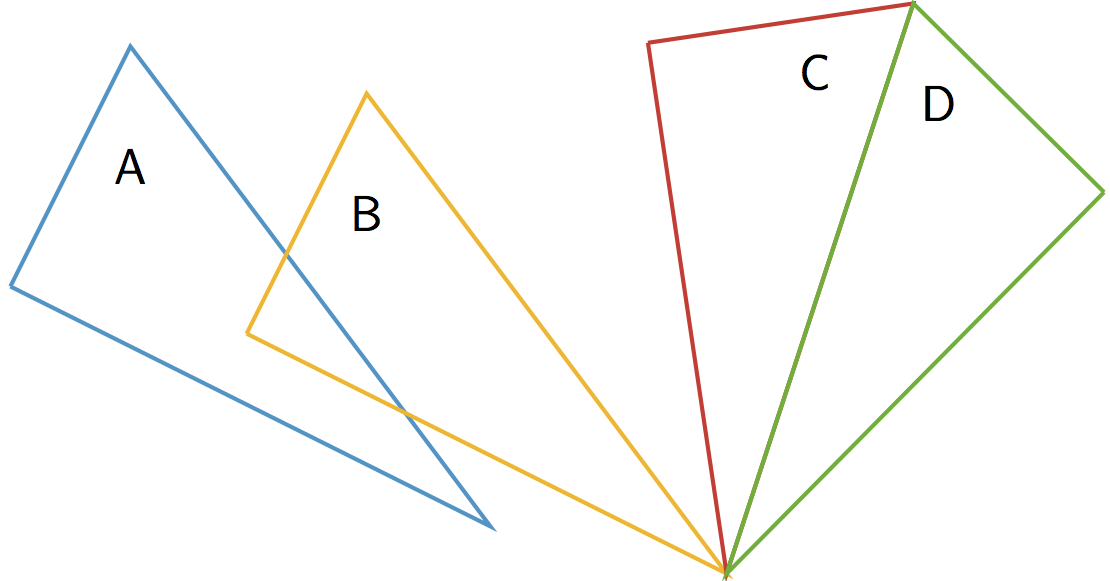
Name a transformation that takes Figure A to Figure B. Name a transformation that takes Figure B to Figure C.
What is one sequence of transformations that takes Figure A to Figure C? Explain how you know.
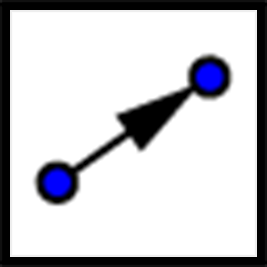
Translate

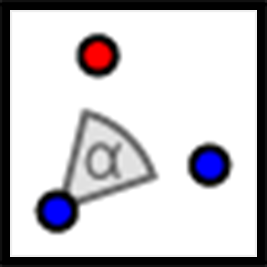
Rotate
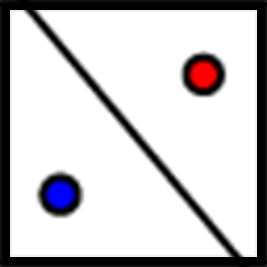
Reflect
Experiment with some other ways to take Figure $A$ to Figure $C$. For example, can you do it with. . .
A move, or combination of moves, is called a transformation. When we do one or more moves in a row, we often call that a sequence of transformations. To distinguish the original figure from its image, points in the image are sometimes labeled with the same letters as the original figure, but with the symbol $’$ attached, as in $A’$ (pronounced “A prime”).
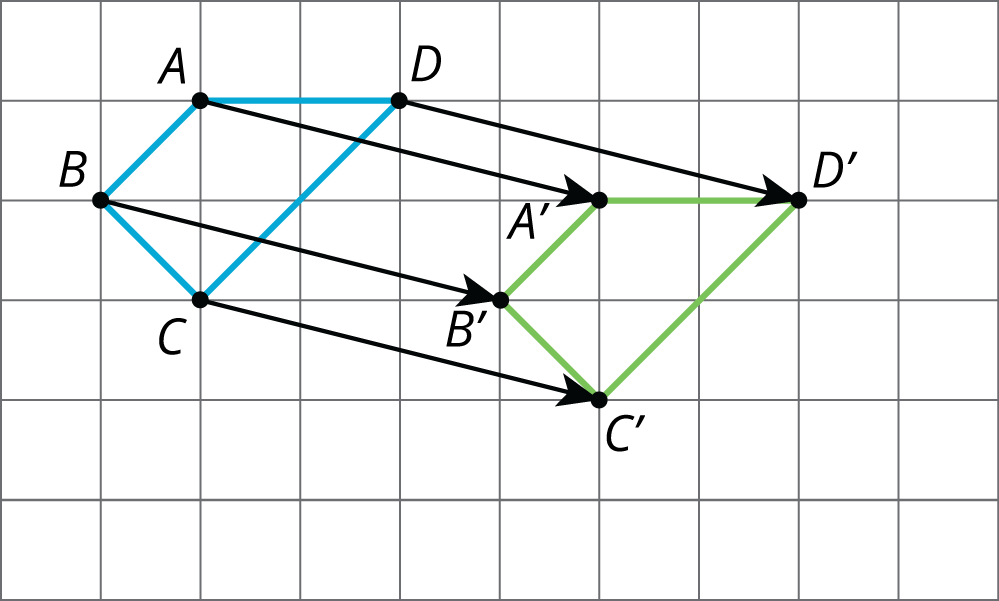
A translation can be described by two points. If a translation moves point $A$ to point $A’$, it moves the entire figure the same distance and direction as the distance and direction from $A$ to $A’$. The distance and direction of a translation can be shown by an arrow.
For example, here is a translation of quadrilateral $ABCD$ that moves $A$ to $A’$.
For example, hexagon $ABCDEF$ is rotated $90^\circ$ counterclockwise using center $P$.
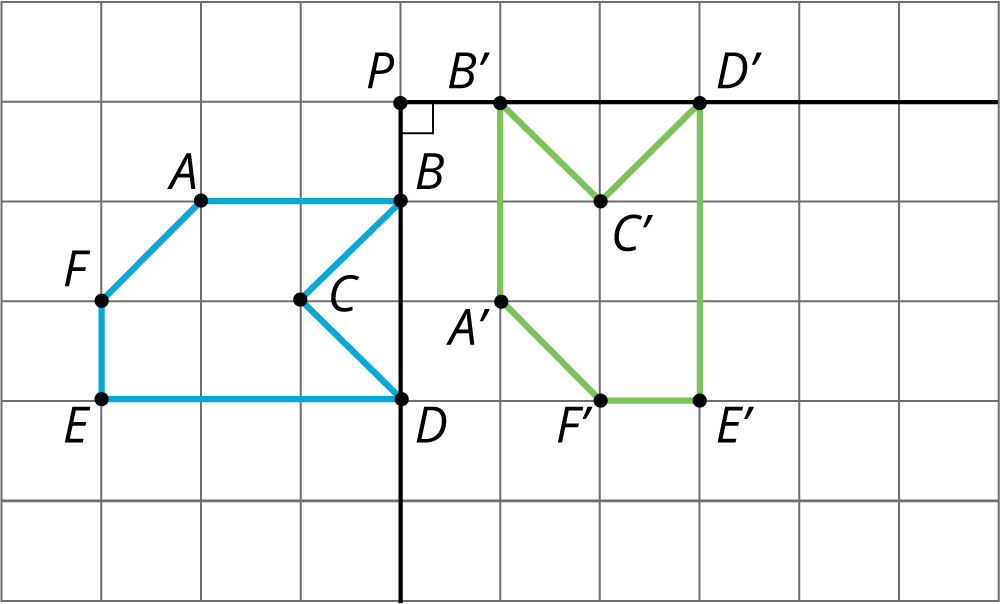
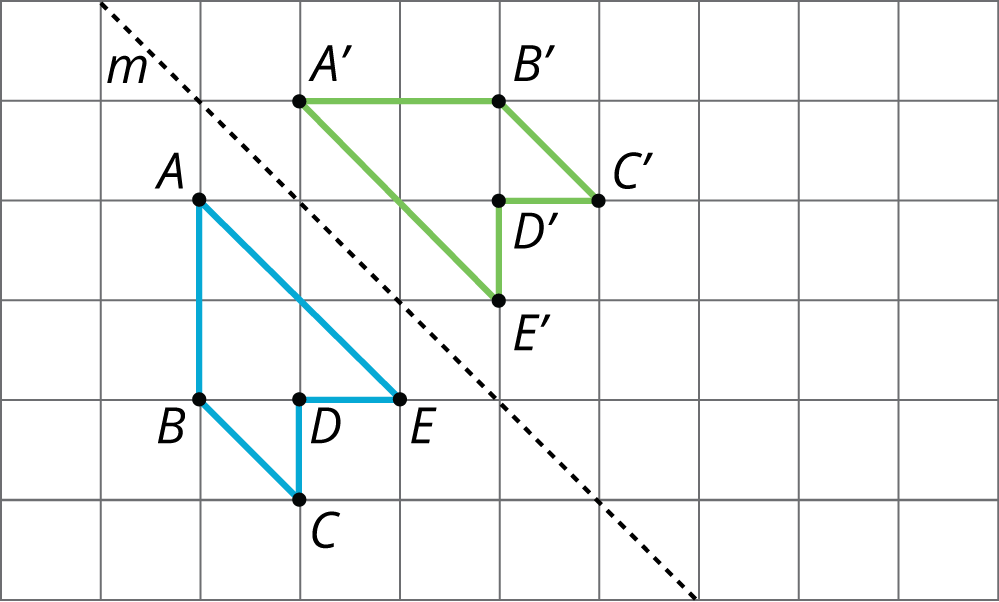
For example, pentagon $ABCDE$ is reflected across line $m$.
A transformation is a translation, rotation, reflection, or dilation, or combination of these. There is also a more general concept of a transformation of the plane that is not discussed in grade 8.
A sequence of transformations is a set of translations, rotations, reflections, and dilations performed in a particular order on a geometric figure, resulting in a final figure.
The diagram shows a sequence of transformations consisting of a translation (from A to B) followed by a rotation (from B to C) followed by a reflection (from C to D). The last triangle is the final figure resulting from the sequence.