Lesson 8: Similar Triangles

Let’s look at similar triangles.

8.1: Equivalent Expressions

Create three different expressions that are each equal to 20. Each expression should include only these three numbers: $4$, $\text- 2$, and $10$.

8.2: Making Pasta Angles and Triangles

Your teacher will give you some dried pasta and a set of angles.

  1. Create a triangle using three pieces of pasta and angle $A$. Your triangle must include the angle you were given, but you are otherwise free to make any triangle you like. Tape your pasta triangle to a sheet of paper so it won’t move.
    1. After you have created your triangle, measure each side length with a ruler and record the length on the paper next to the side. Then measure the angles to the nearest 5 degrees using a protractor and record these measurements on your paper.

    2. Find two others in the room who have the same angle $A$ and compare your triangles. What is the same? What is different? Are the triangles congruent? Similar?

    3. How did you decide if they were or were not congruent or similar?
  2. Now use more pasta and angles $A$, $B$, and $C$ to create another triangle. Tape this pasta triangle on a separate sheet of paper.
    1. After you have created your triangle, measure each side length with a ruler and record the length on the paper next to the side. Then measure the angles to the nearest 5 degrees using a protractor and record these measurements on your paper.

    2. Find two others in the room who used your same angles and compare your triangles. What is the same? What is different? Are the triangles congruent? Similar?

    3. How did you decide if they were or were not congruent or similar?

  3. Here is triangle $PQR$. Break a new piece of pasta, different in length than segment $PQ$.

    • Tape the piece of pasta so that it lays on top of line $PQ$ with one end of the pasta at $P$ (if it does not fit on the page, break it further). Label the other end of the piece of pasta $S$.
    • Tape a full piece of pasta, with one end at $S$, making an angle congruent to $\angle PQR$.
    • Tape a full piece of pasta on top of line $PR$ with one end of the pasta at $P$. Call the point where the two full pieces of pasta meet $T$.

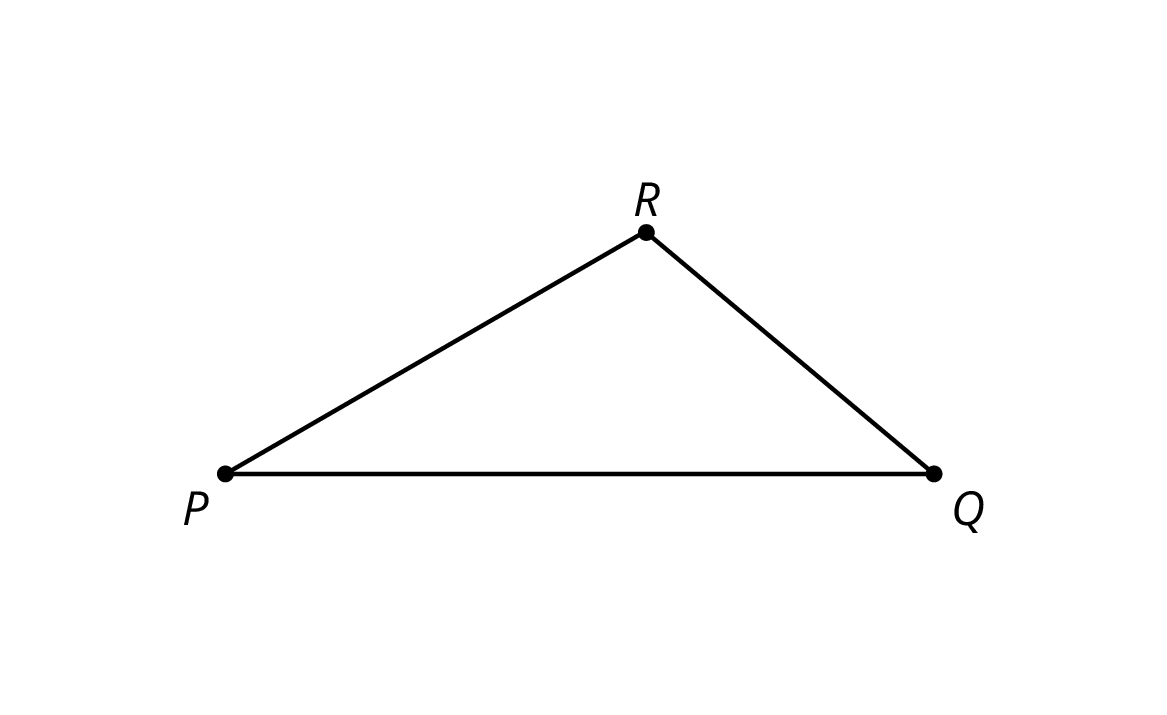
    1. Is your new pasta triangle $PST$ similar to $\triangle PQR$? Explain your reasoning.

    2. If your broken piece of pasta were a different length, would the pasta triangle still be similar to $\triangle PQR$? Explain your reasoning.

8.3: Similar Figures in a Regular Pentagon

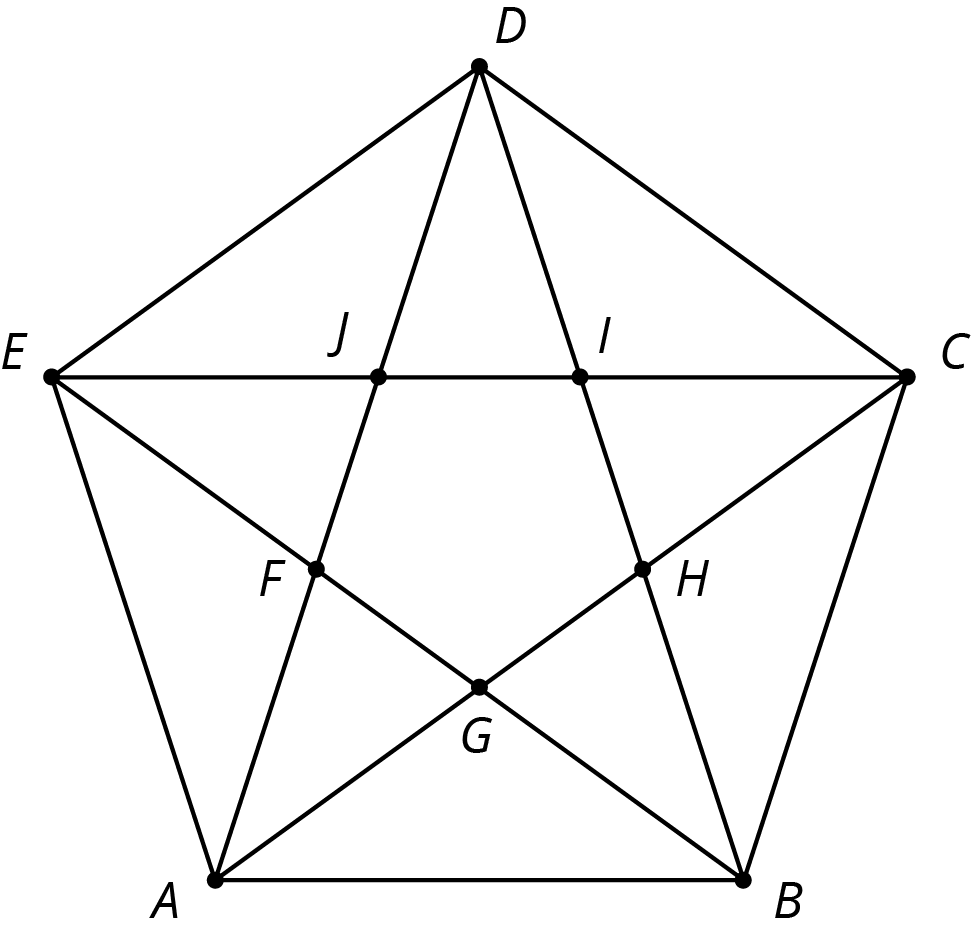
  1. This diagram has several triangles that are similar to triangle $DJI$.

    1. Three different scale factors were used to make triangles similar to $DJI$. In the diagram, find at least one triangle of each size that is similar to $DJI$.
    2. Explain how you know each of these three triangles is similar to $DJI$.
  2. Find a triangle in the diagram that is not similar to $DJI$.

Summary

We learned earlier that two polygons are similar when there is a sequence of translations, rotations, reflections, and dilations taking one polygon to the other. When the polygons are triangles, we only need to check that that both triangles have two corresponding angles to show they are similar—can you tell why?

Here is an example. Triangle $ABC$ and triangle $DEF$ each have a 30 degree angle and a 45 degree angle.

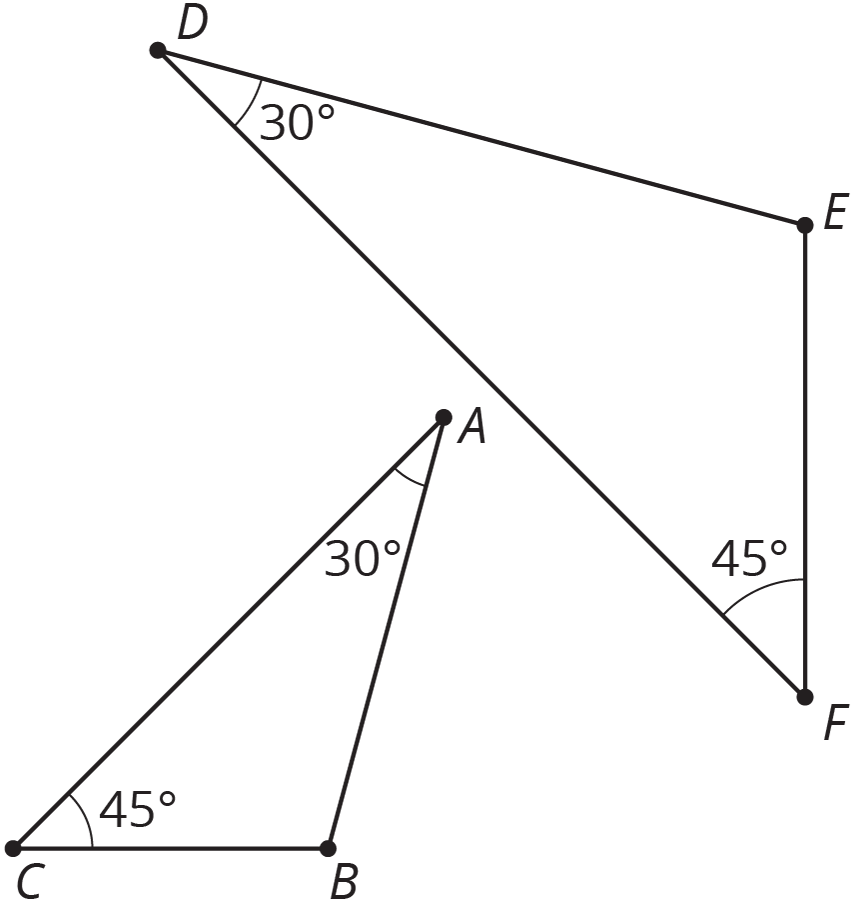
We can translate $A$ to $D$ and then rotate so that the two 30 degree angles are aligned, giving this picture:

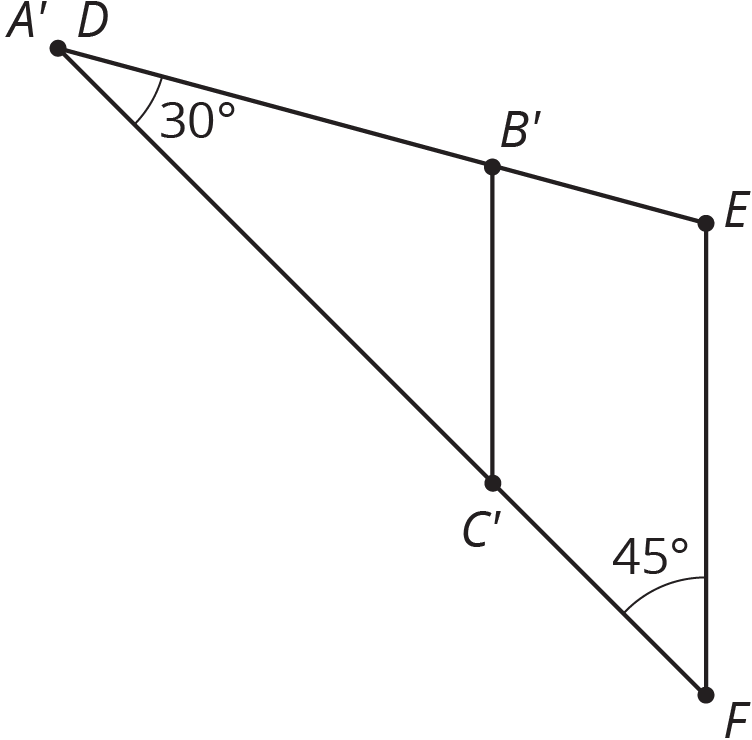Now a dilation with center $D$ and appropriate scale factor will move $C'$ to $F$. This dilation also moves $B'$ to $E$, showing that triangles $ABC$ and $DEF$ are similar.

Practice Problems ▶