Lesson 13: The Volume of a Cylinder

Let’s explore cylinders and their volumes.

13.1: A Circle's Dimensions

A circle with the center labeled A. Points B, C, and D lie on the circle, where B is to the right of A, C is to the left of A, and point D is above and to the left of A. A line segment is drawn from A to D and is labeled 4. Another line segment is drawn from B to C such that the segment goes through A.

Here is a circle. Points A, B, C, and D are drawn, as well as Segments AD and BC.

  1. What is the area of the circle, in square units? Select all that apply.
    1. 4\pi
    2. \pi 8
    3. 16\pi
    4. \pi 4^2
    5. approximately 25
    6. approximately 50
  2. If the area of a circle is 49\pi square units, what is its radius? Explain your reasoning.

13.2: Circular Volumes

What is the volume of each figure, in cubic units? Even if you aren’t sure, make a reasonable guess.

  1. Figure A: A rectangular prism whose base has an area of 16 square units and whose height is 3 units.
  2. Figure B: A cylinder whose base has an area of 16\pi square units and whose height is 1 unit.
  3. Figure C: A cylinder whose base has an area of 16\pi square units and whose height is 3 units.

13.3: A Cylinder's Dimensions

  1. For cylinders A–D, sketch a radius and the height. Label the radius with an r and the height with an h.

    A collection of six cylinder images labeled "A" through "F". Image "A" is the drawing of a cylinder that lies on its bottom base; Image "B" is the drawing of solid, green cylinder tilted to the right; Image "C" is an image of an oatmeal container in the shape of a cylinder; Image "D" is the drawing of a cylinder that lies on its rectangular face; Image "E" is an image of a tanker, 18-wheeler truck which in the shape of a cylinder Image "F" is an image of a farm grain silo that is in the shape of a cylinder. Silo, Water Tank Volvo water tank truck in Iraq Copyright Owner: Jum Gordon, N3dling License: Public Domain Via: Pixabay
  2. Earlier you learned how to sketch a cylinder. Sketch cylinders for E and F and label each one’s radius and height.

13.4: A Cylinder's Volume

  1. Here is a cylinder with height 4 units and diameter 10 units.

    A right circular cylinder with a height of 4 and a diameter of 10.
    1. Shade the cylinder’s base.
    2. What is the area of the cylinder’s base? Express your answer in terms of \pi.
    3. What is the volume of this cylinder? Express your answer in terms of \pi.
  2. A silo is a cylindrical container that is used on farms to hold large amounts of goods, such as grain. On a particular farm, a silo has a height of 18 feet and diameter of 6 feet. Make a sketch of this silo and label its height and radius. How many cubic feet of grain can this silo hold? Use 3.14 as an approximation for \pi.

Summary

We can find the volume of a cylinder with radius r and height h using two ideas we've seen before:

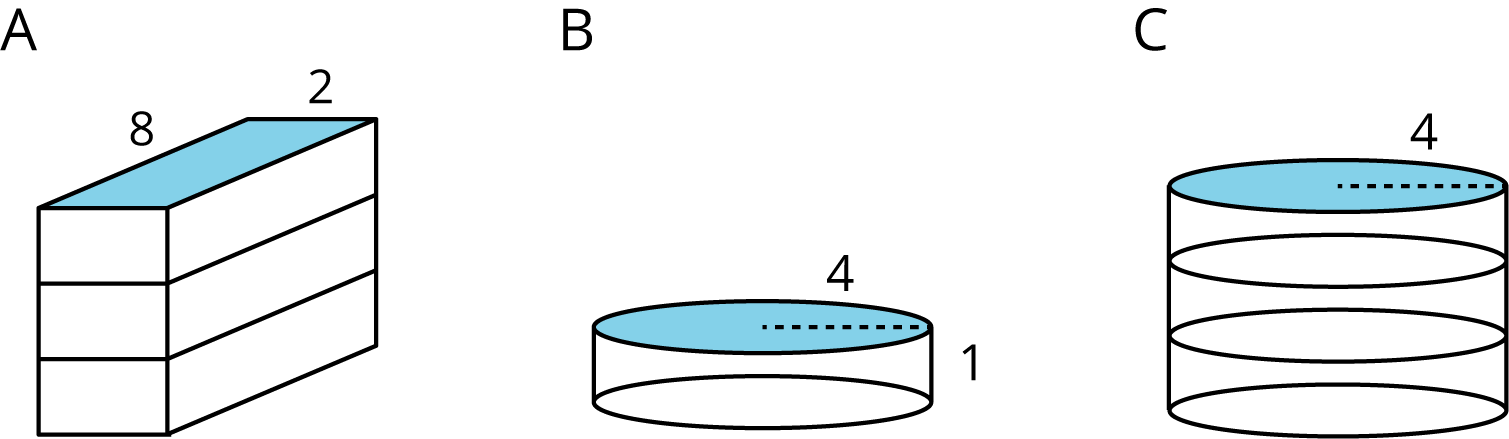
  • The volume of a rectangular prism is a result of multiplying the area of its base by its height.
  • The base of the cylinder is a circle with radius r, so the base area is \pi r^2.

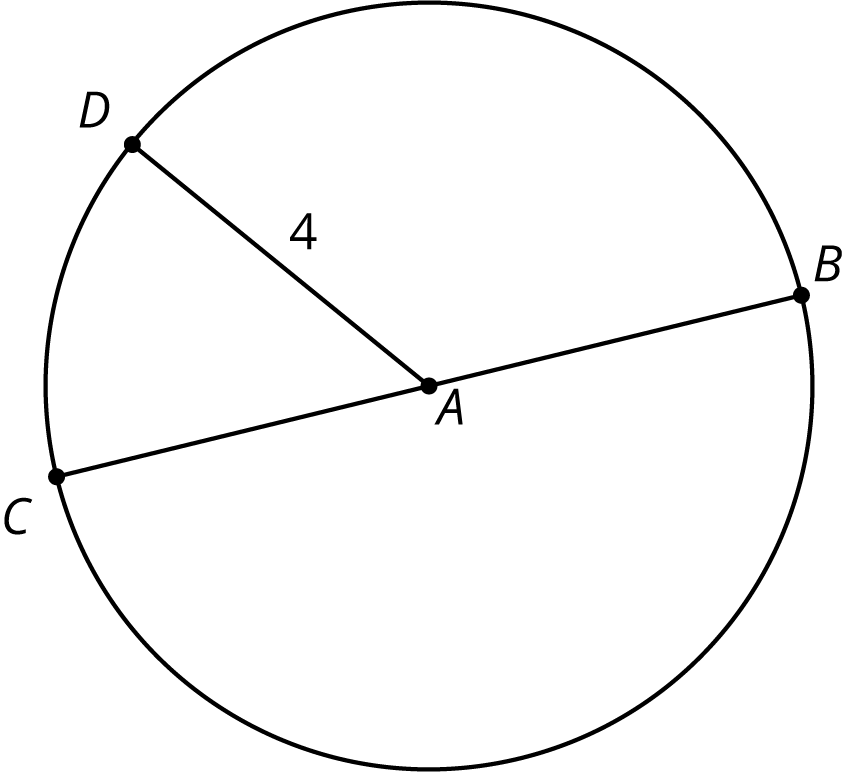
Remember that \pi is the number we get when we divide the circumference of any circle by its diameter. The value of \pi is approximately 3.14.

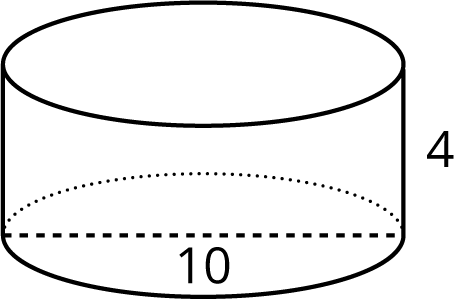
Just like a rectangular prism, the volume of a cylinder is the area of the base times the height. For example, take a cylinder whose radius is 2 cm and whose height is 5 cm.

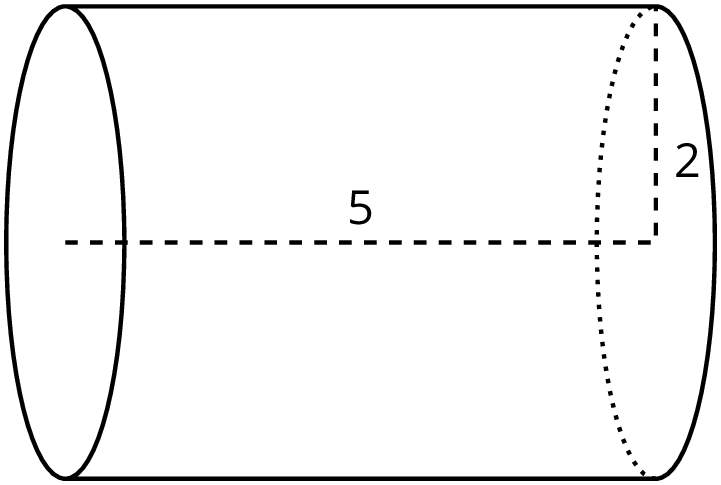
A drawing of a cylinder whose radius is 2 and height is 5.

The base has an area of 4\pi cm2 (since \pi\boldcdot 2^2=4\pi), so the volume is 20\pi cm3 (since 4\pi \boldcdot 5 = 20\pi). Using 3.14 as an approximation for \pi, we can say that the volume of the cylinder is approximately 62.8 cm3.

In general, the base of a cylinder with radius r units has area \pi r^2 square units. If the height is h units, then the volume V in cubic units is V=\pi r^2h

Practice Problems ▶