11.1: Coordinates and Lengths in the Coordinate Plane
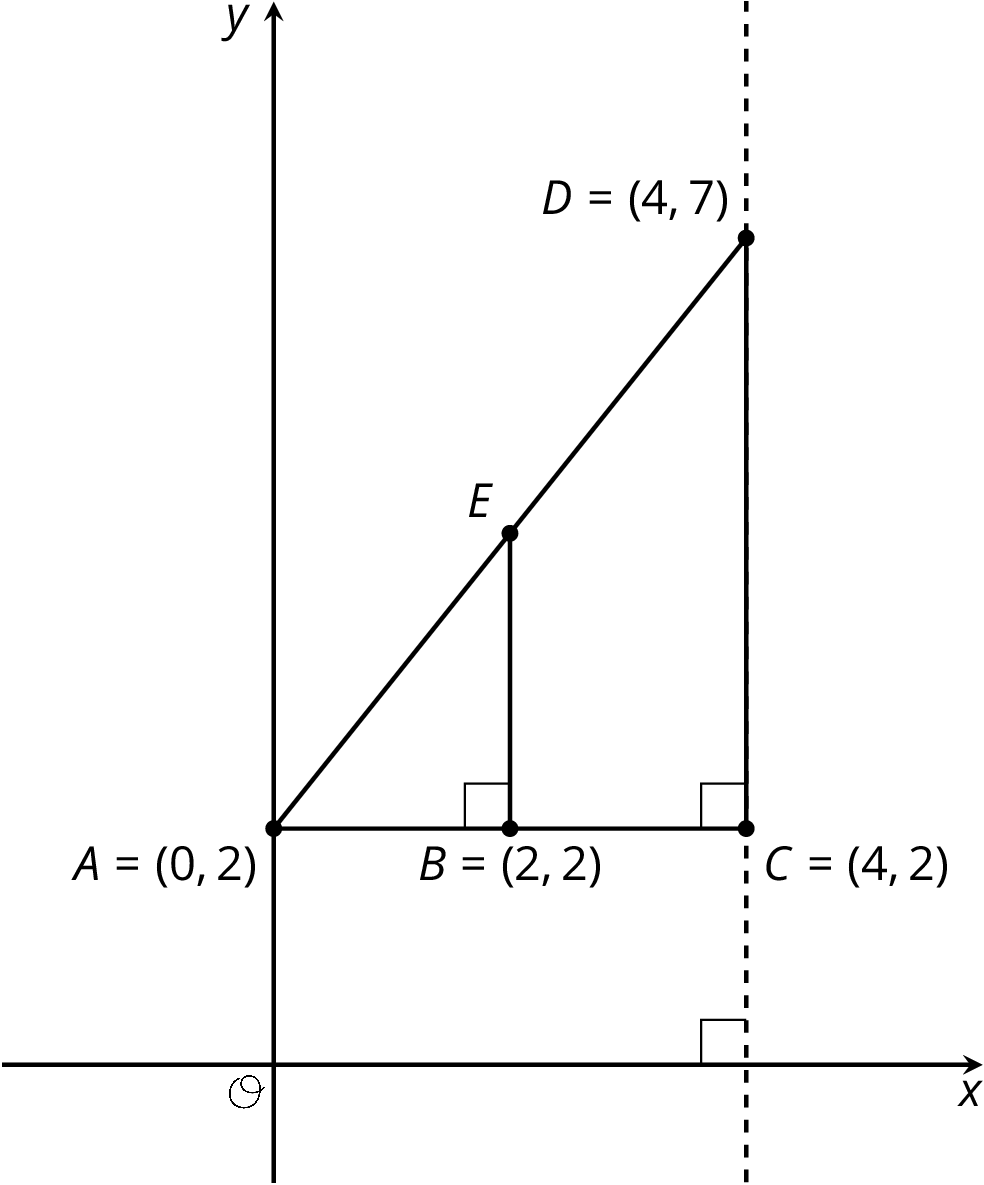
Find each of the following and explain your reasoning:
- The length of segment $BE$.
- The coordinates of $E$.
Let’s explore the relationship between points on a line and the slope of the line.

Find each of the following and explain your reasoning:
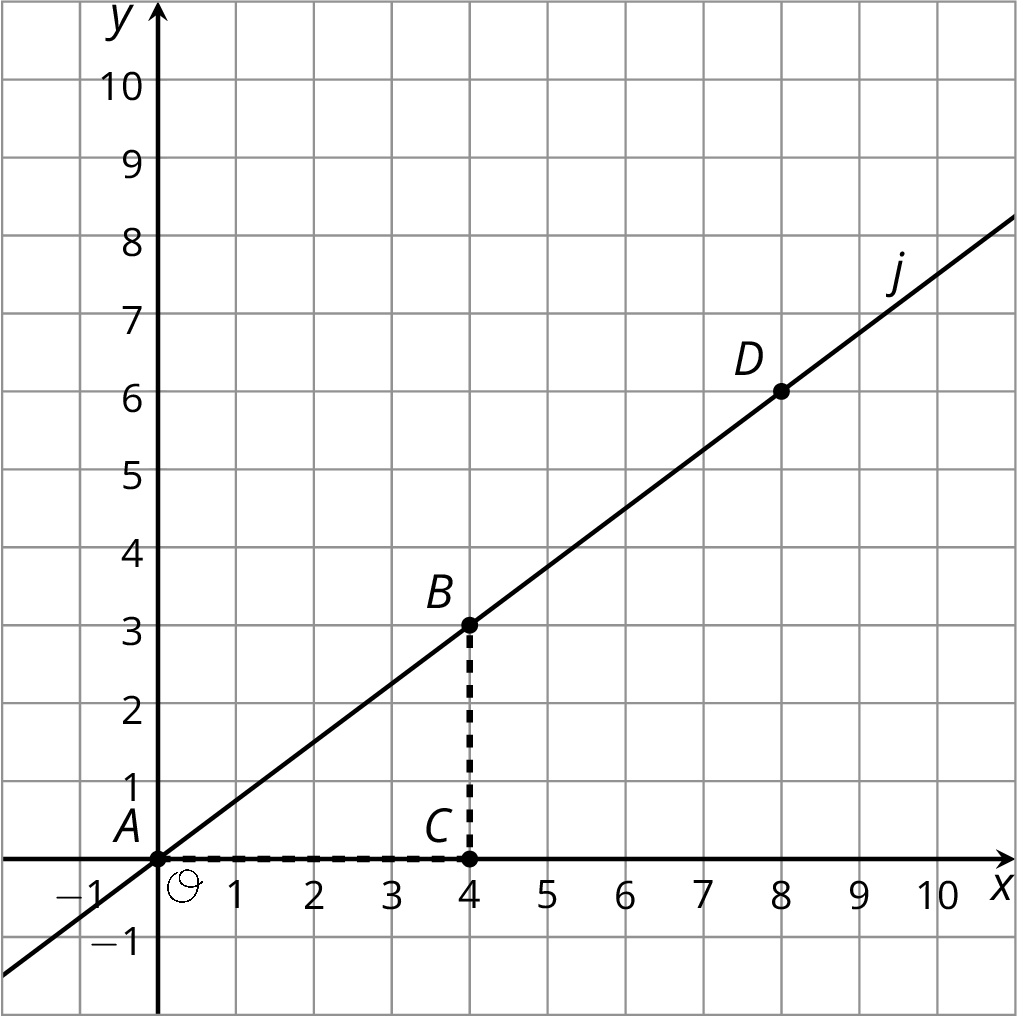
Line $j$ is shown in the coordinate plane.
Is point $(20,15)$ on line $j$? Explain how you know.
Is point $(100,75)$ on line $j$? Explain how you know.
Is point $(90,68)$ on line $j$? Explain how you know.
Suppose you know the $x$- and $y$-coordinates of a point. Write a rule that would allow you to test whether the point is on line $j$.
Here are two diagrams:
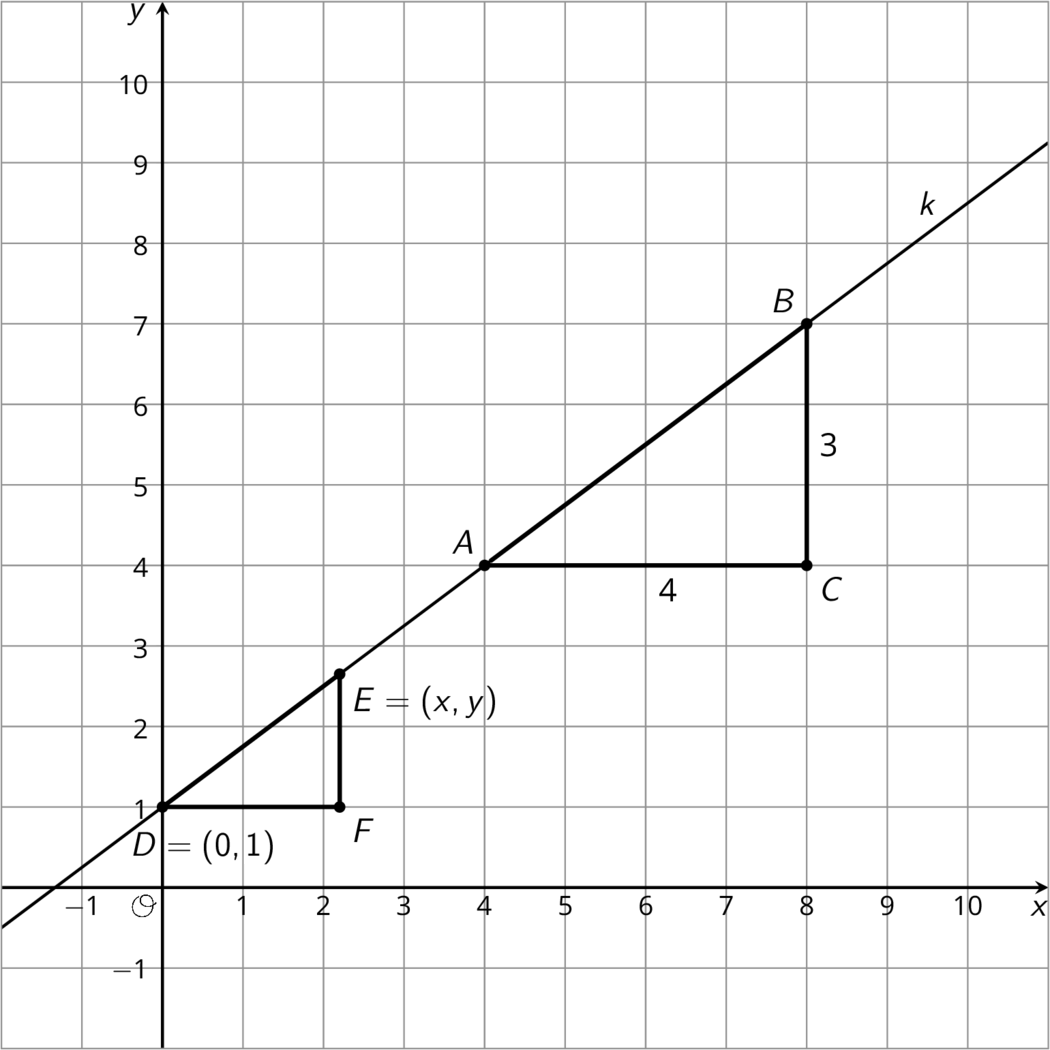

Here are the points $A$, $C$, and $E$ on the same line. Triangles $ABC$ and $ADE$ are slope triangles for the line so we know they are similar triangles. Let’s use their similarity to better understand the relationship between $x$ and $y$, which make up the coordinates of point $E$.
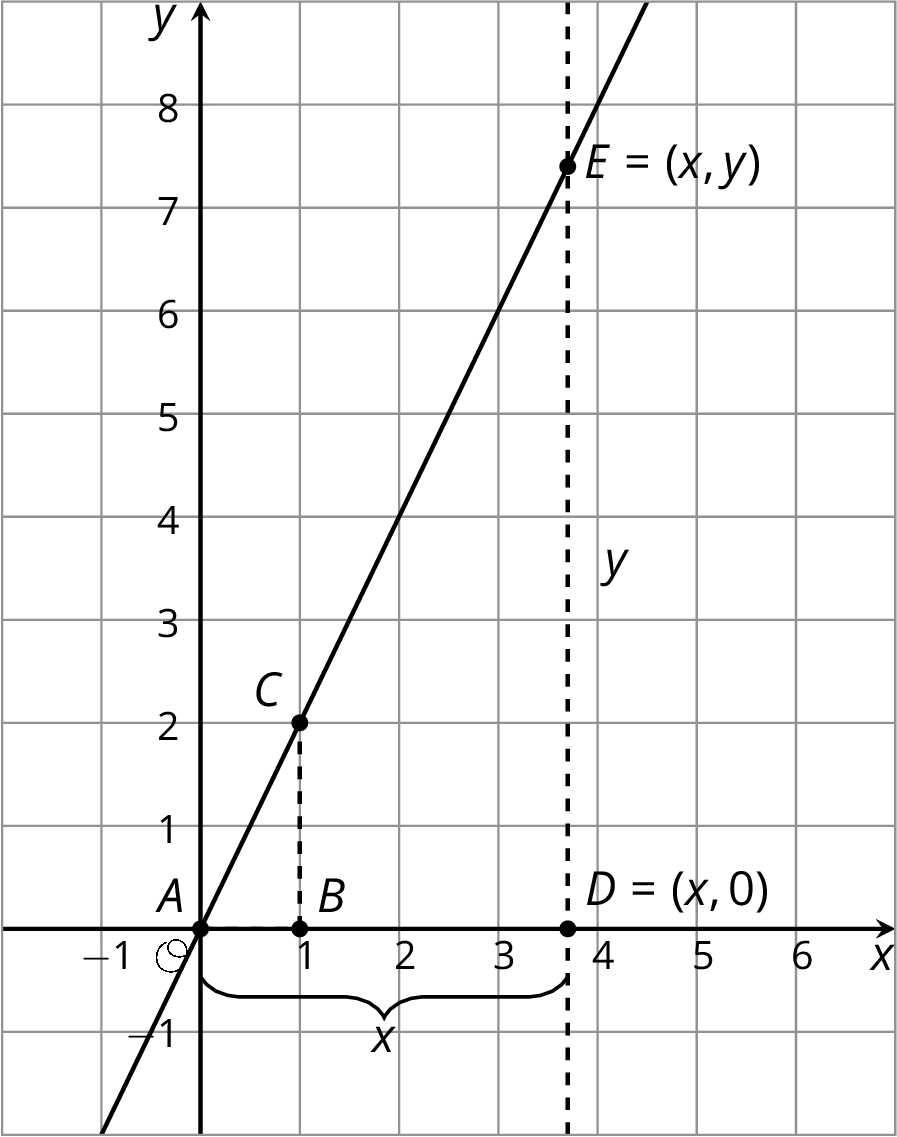
The slope for triangle $ABC$ is $\frac{2}{1}$ since the vertical side has length 2 and the horizontal side has length 1. The slope we find for triangle $ADE$ is $\frac{y}{x}$ because the vertical side has length $y$ and the horizontal side has length $x$. These two slopes must be equal since they are from slope triangles for the same line, and so: $$\frac{2}{1} = \frac{y}{x}$$
Here are two different slope triangles. We can use the same reasoning to describe the relationship between $x$ and $y$ for this point $E$.
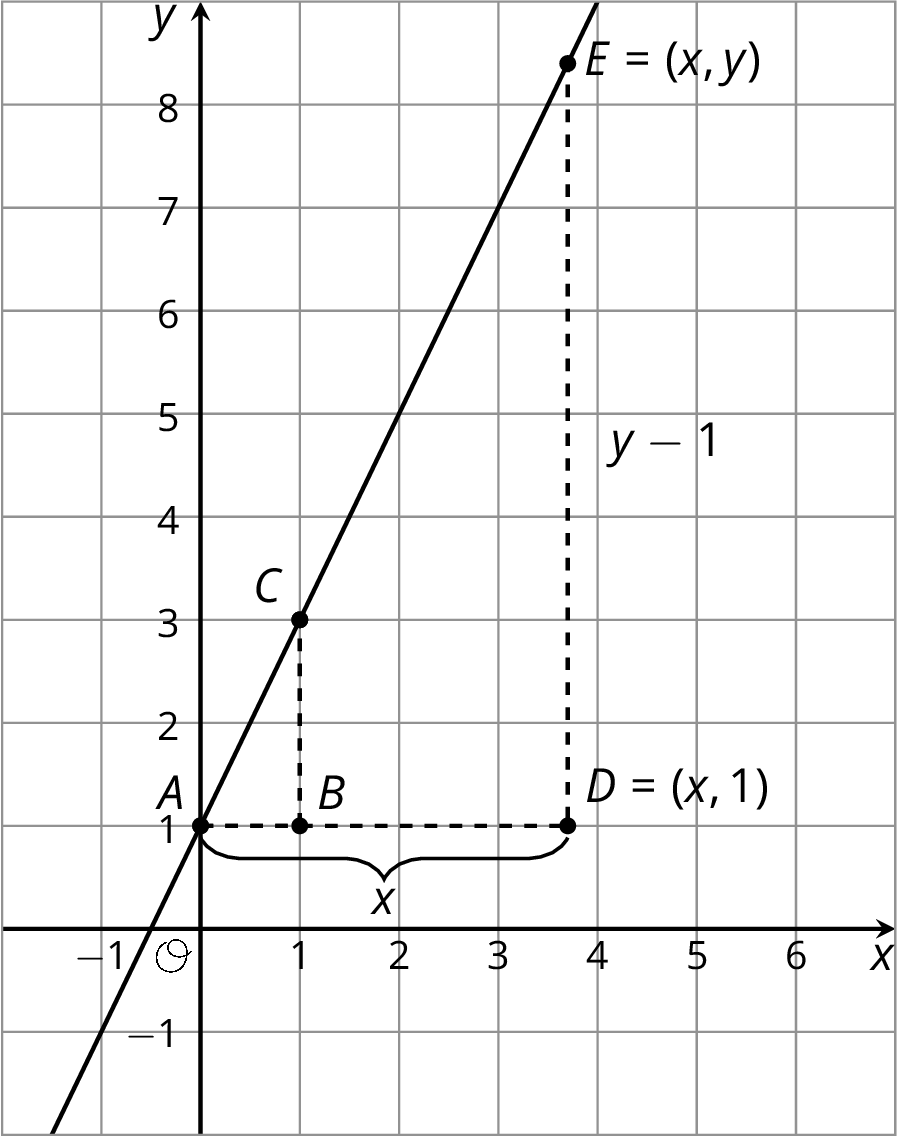
The slope for triangle $ABC$ is $\frac{2}{1}$ since the vertical side has length 2 and the horizontal side has length 1. For triangle $ADE$, the horizontal side has length $x$. The vertical side has length $y-1$ because the distance from $(x,y)$ to the $x$-axis is $y$ but the vertical side of the triangle stops 1 unit short of the $x$-axis. So the slope we find for triangle $ADE$ is $\frac{y-1}{x}$. The slopes for the two slope triangles are equal, meaning: $$\frac{2}{1} = \frac{y-1}{x}$$
Since $y-1$ is twice $x$, another way to write this equation is $y-1 = 2x$. This equation is true for any point $(x,y)$ on the line!