4.1: Estimating a Scale Factor
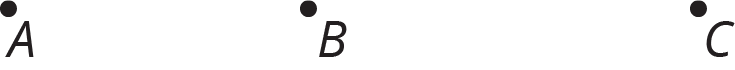
Point $C$ is the dilation of point $B$ with center of dilation $A$ and scale factor $s$. Estimate $s$. Be prepared to explain your reasoning.
Let’s dilate figures on a rectangular grid.
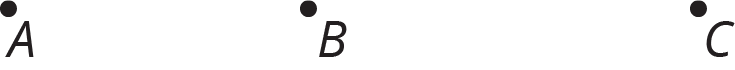
Point $C$ is the dilation of point $B$ with center of dilation $A$ and scale factor $s$. Estimate $s$. Be prepared to explain your reasoning.

Your teacher will give you some cards. Each of Cards 1 through 6 shows a figure in the coordinate plane and describes a dilation.
Each of Cards A through E describes the image of the dilation for one of the numbered cards.
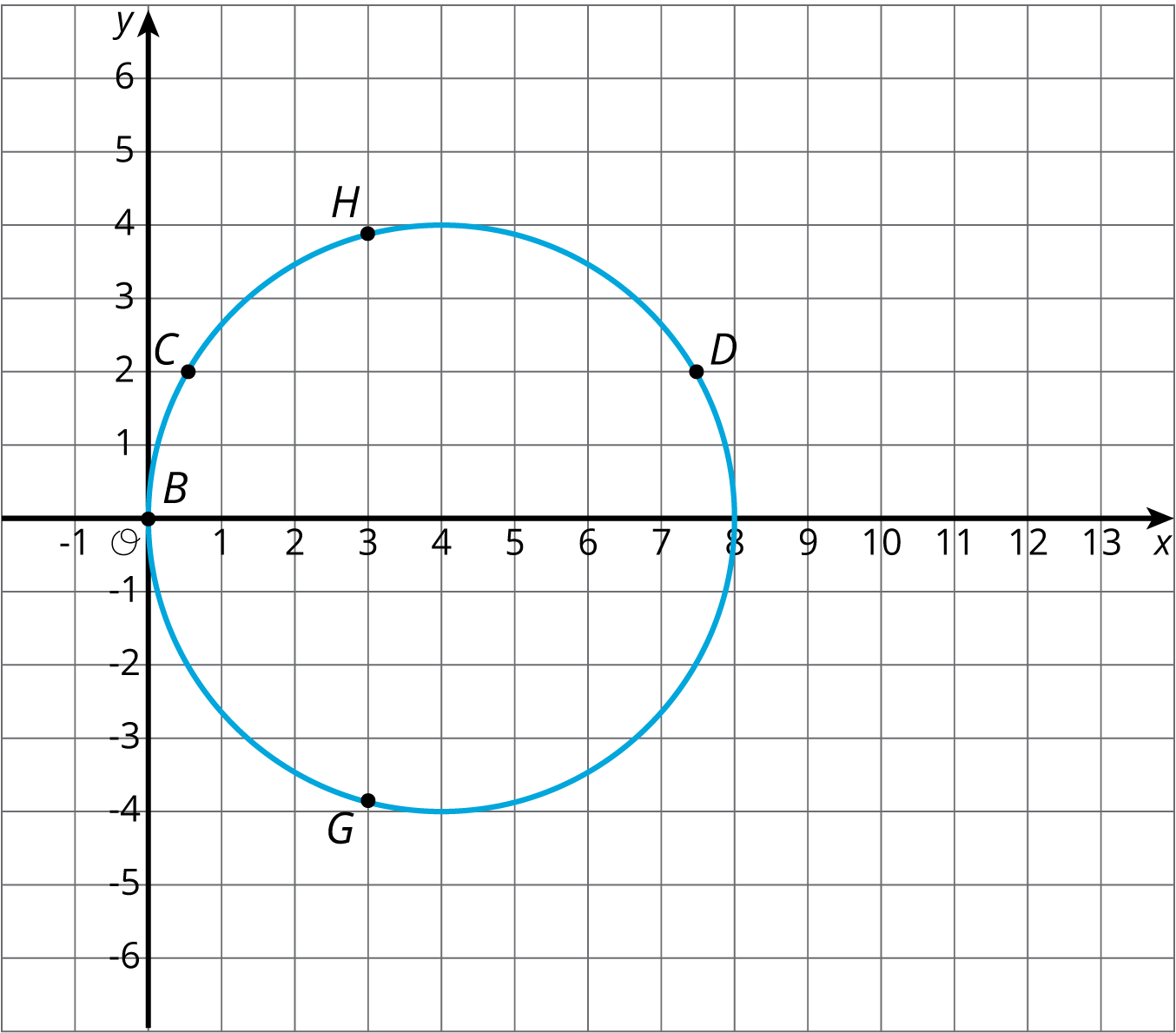
The image of a circle under dilation is a circle when the center of the dilation is the center of the circle. What happens if the center of dilation is a point on the circle? Using center of dilation $(0,0)$ and scale factor 1.5, dilate the circle shown on the diagram. This diagram shows some points to try dilating.
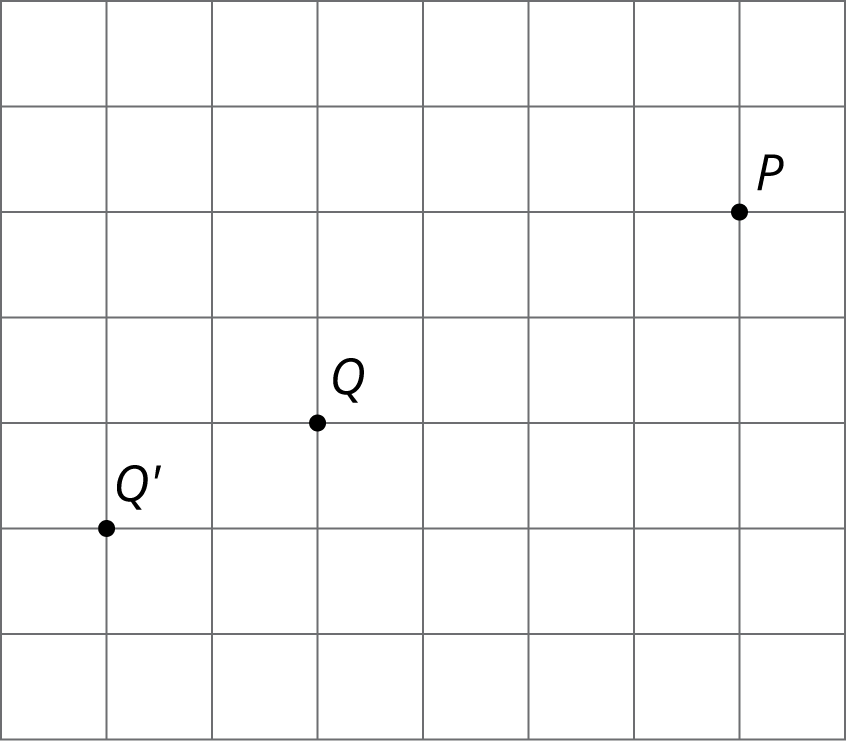
Square grids can be useful for showing dilations. The grid is helpful especially when the center of dilation and the point(s) being dilated lie at grid points. Rather than using a ruler to measure the distance between the points, we can count grid units.
For example, suppose we want to dilate point $Q$ with center of dilation $P$ and scale factor $\frac{3}{2}$. Since $Q$ is 4 grid squares to the left and 2 grid squares down from $P$, the dilation will be 6 grid squares to the left and 3 grid squares down from $P$ (can you see why?). The dilated image is marked as $Q’$ in the picture.
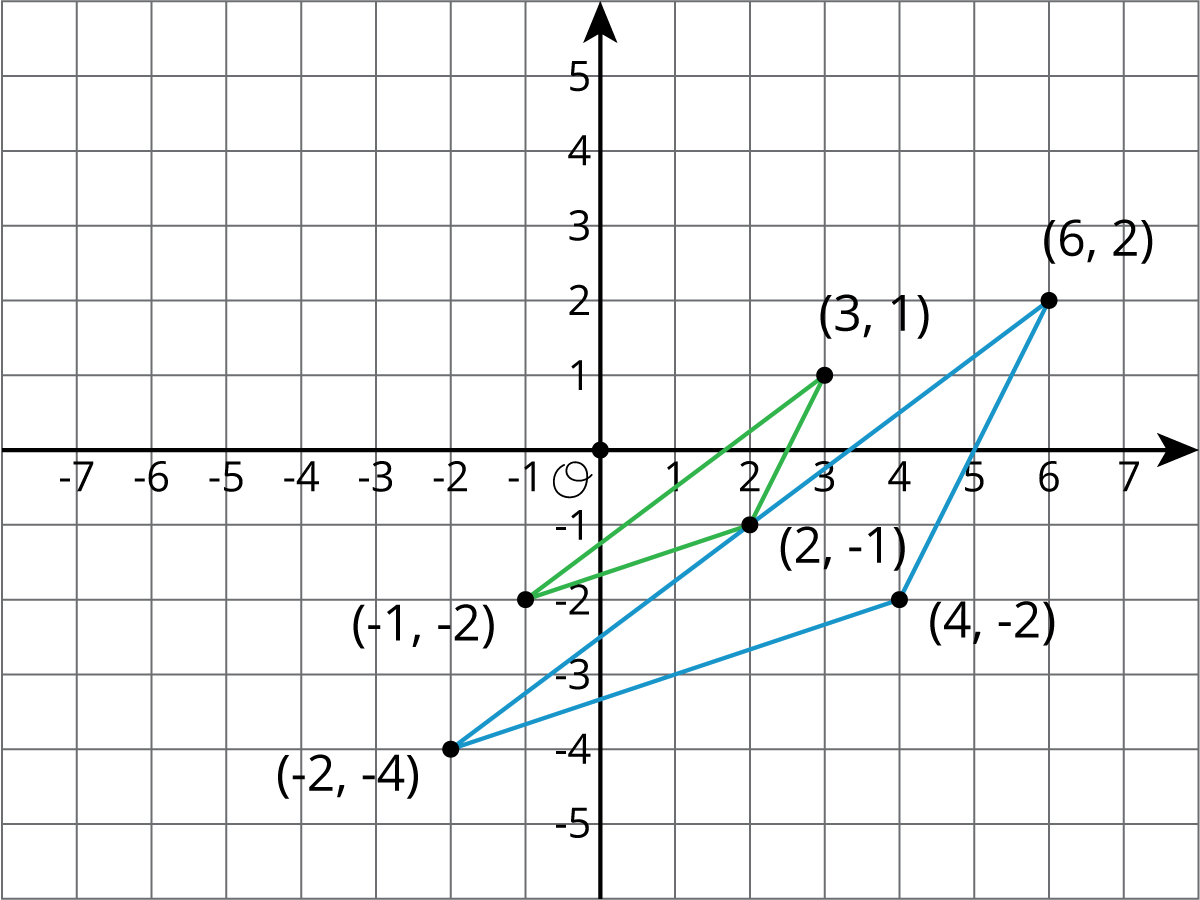
Sometimes the square grid comes with coordinates. The coordinate grid gives us a convenient way to name points, and sometimes the coordinates of the image can be found with just arithmetic.
For example, to make a dilation with center $(0,0)$ and scale factor 2 of the triangle with coordinates $(\text-1, \text- 2)$, $(3,1)$, and $(2, \text- 1)$, we can just double the coordinates to get $(\text- 2, \text- 4)$, $(6,2)$, and $(4, \text- 2)$.