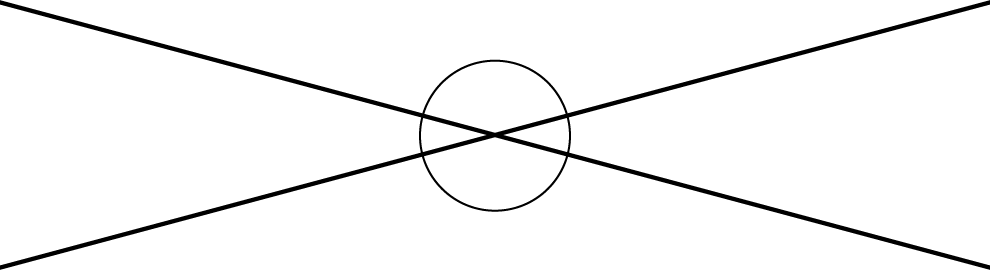
9.1: Line Moves
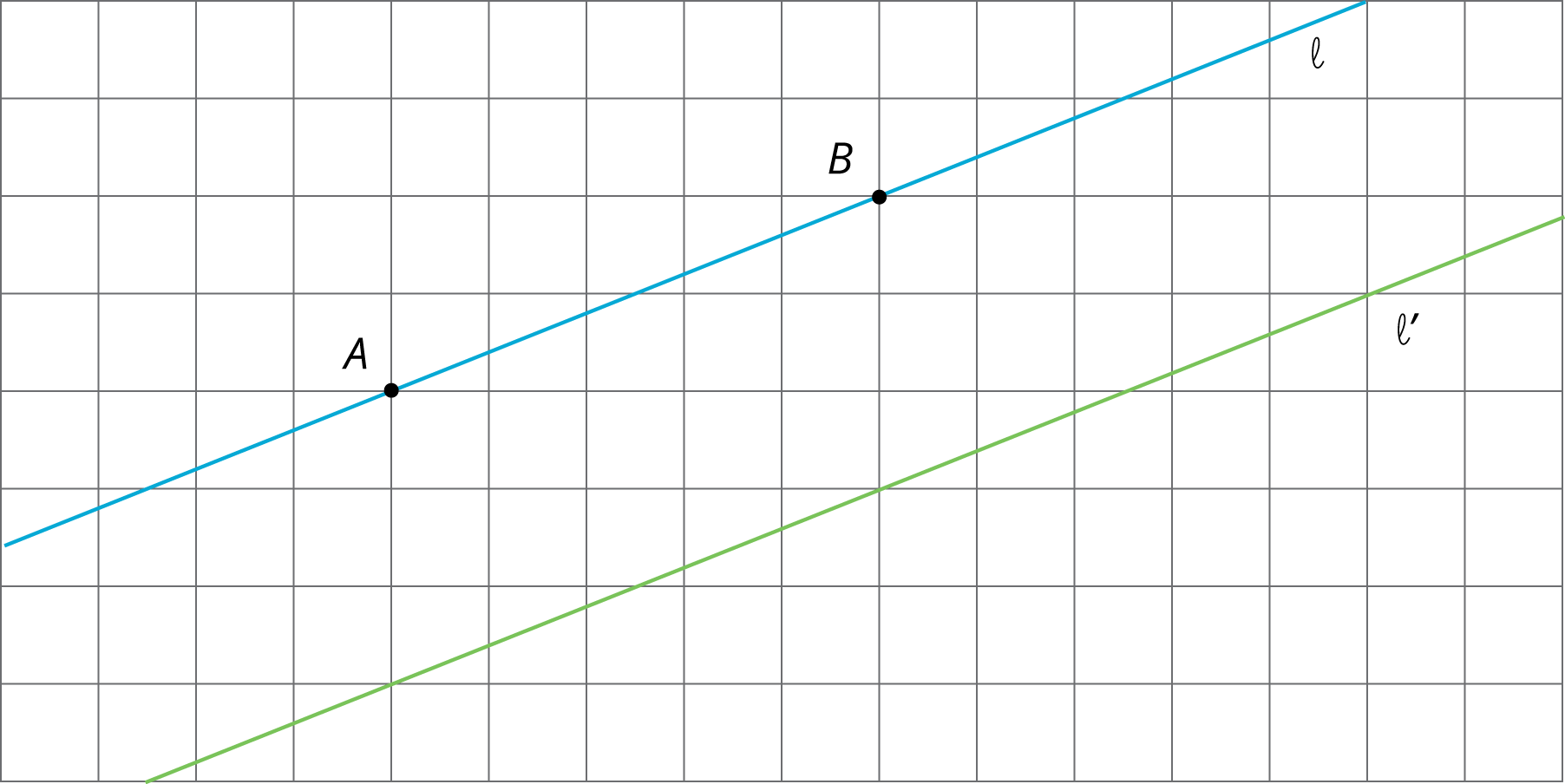
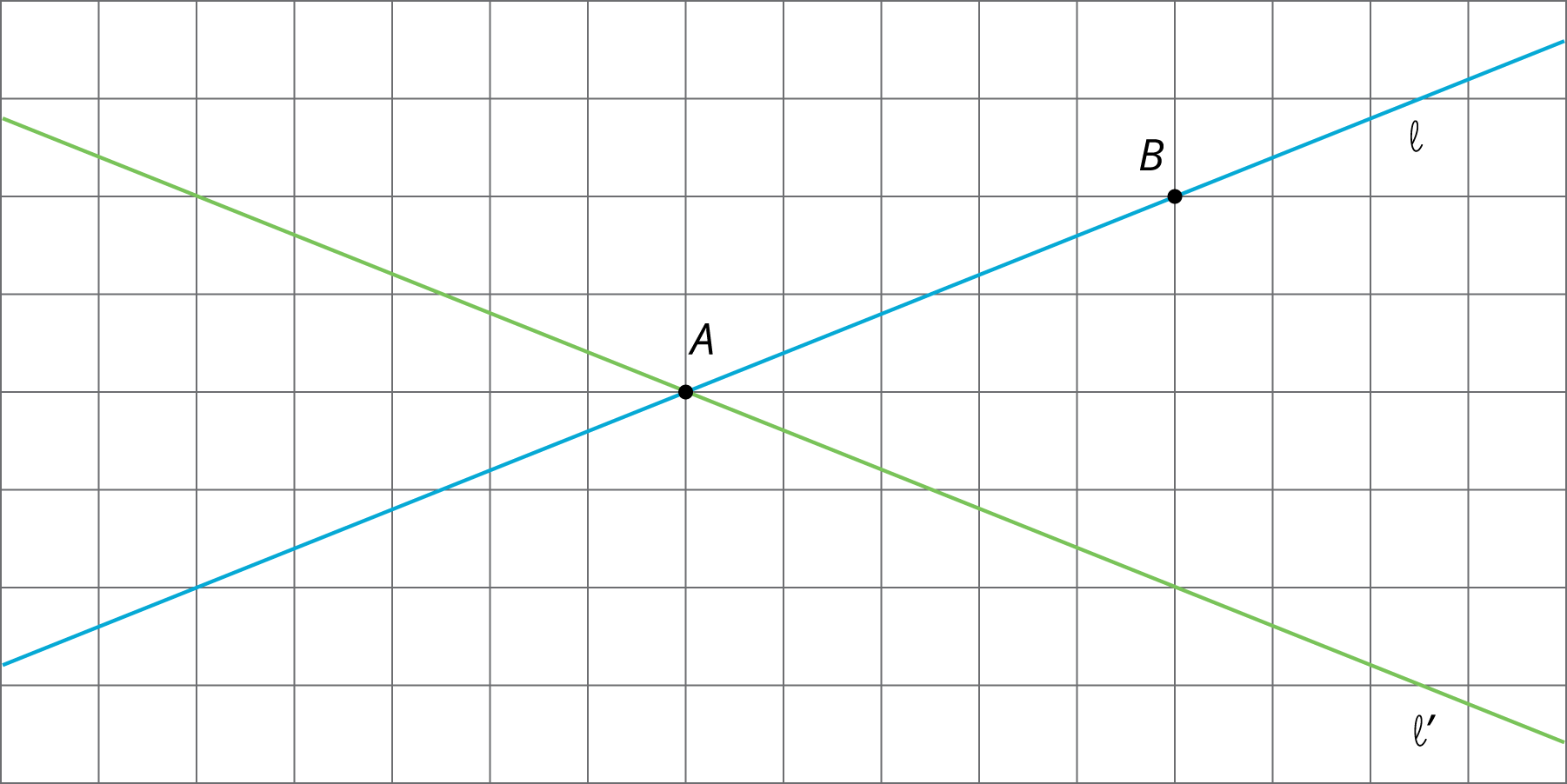
For each diagram, describe a translation, rotation, or reflection that takes line $\ell$ to line $\ell’$. Then plot and label $A’$ and $B’$, the images of $A$ and $B$.
Let’s transform some lines.
For each diagram, describe a translation, rotation, or reflection that takes line $\ell$ to line $\ell’$. Then plot and label $A’$ and $B’$, the images of $A$ and $B$.
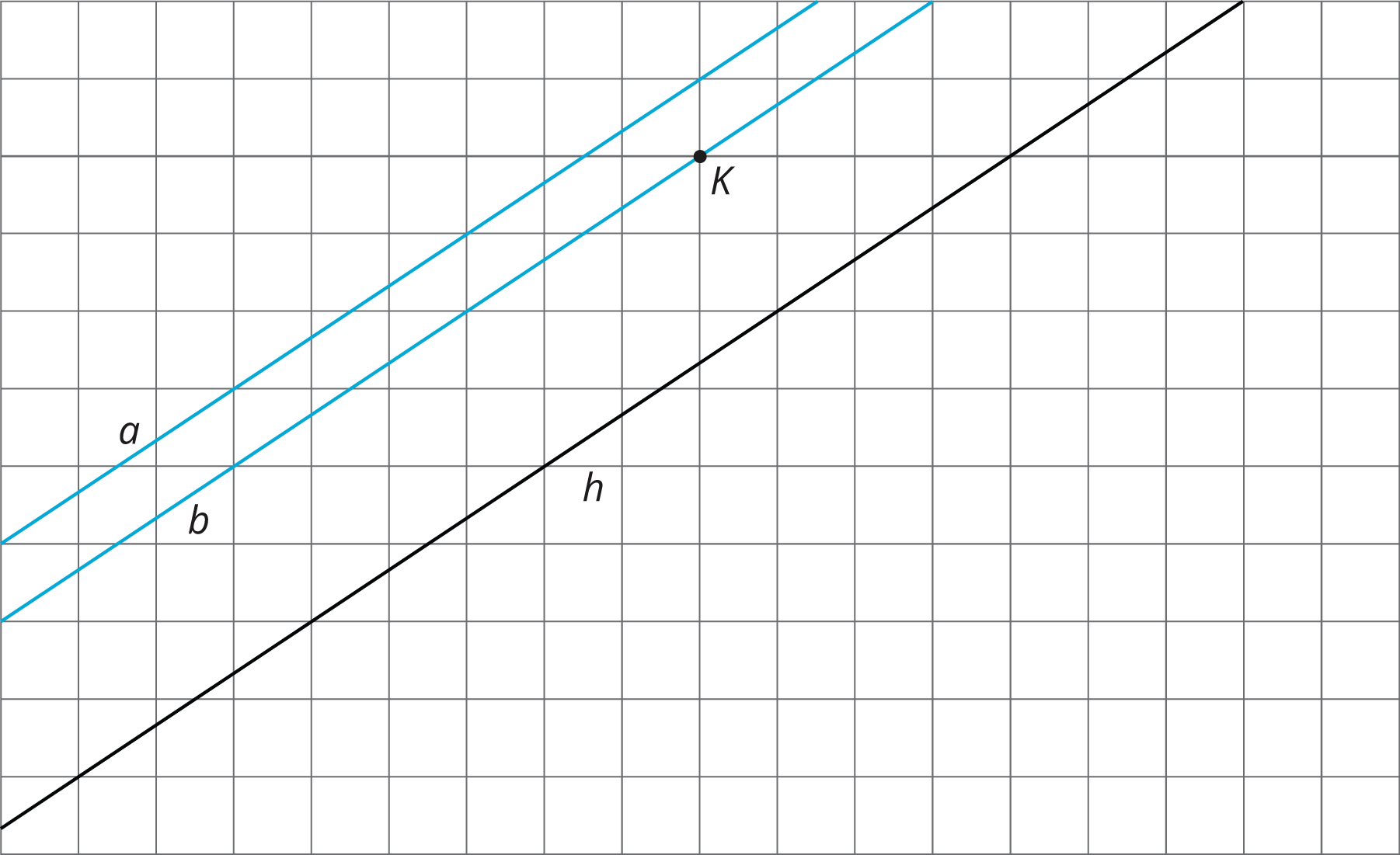
Use a piece of tracing paper to trace lines $a$ and $b$ and point $K$. Then use that tracing paper to draw the images of the lines under the three different transformations listed.
As you perform each transformation, think about the question:
What is the image of two parallel lines under a rigid transformation?
Translate lines $a$ and $b$ 3 units up and 2 units to the right.
Rotate lines $a$ and $b$ counterclockwise 180 degrees using $K$ as the center of rotation.
What is the same in the original and the image?
Reflect lines $a$ and $b$ across line $h$.
When you rotate two parallel lines, sometimes the two original lines intersect their images and form a quadrilateral. What is the most specific thing you can say about this quadrilateral? Can it be a square? A rhombus? A rectangle that isn’t a square? Explain your reasoning.

On the diagram, draw the image of the line and points $A$, $C$, and $B$ after the line has been rotated 180 degrees around point $D$.
Label the images of the points $A’$, $B’$, and $C’$.
What is the order of all seven points? Explain or show your reasoning.

Rotate the figure 180 degrees about point $C$. Label the image of $A$ as $A’$ and the image of $D$ as $D’$.
What do you know about the relationship between angle $CAD$ and angle $CA’D’$? Explain or show your reasoning.
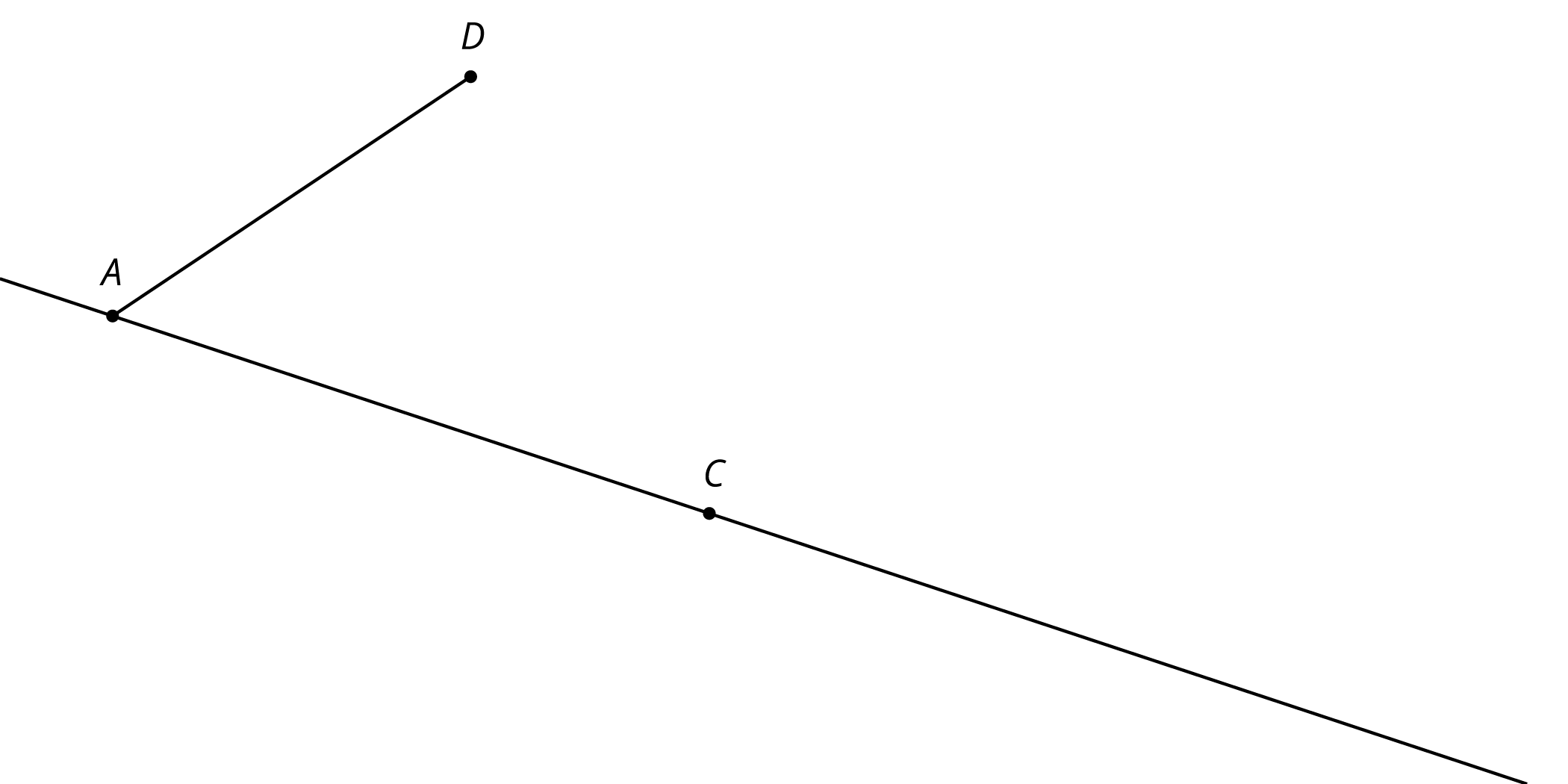
Rotate the figure 180 degrees around $O$. Label the image of $A$ as $A’$ and the image of $D$ as $D’$.
What do you know about the relationship between the angles in the figure? Explain or show your reasoning.
Rigid transformations have the following properties:
A rigid transformation of a line is a line.
A rigid transformation of two parallel lines results in two parallel lines that are the same distance apart as the original two lines.
Sometimes, a rigid transformation takes a line to itself. For example:
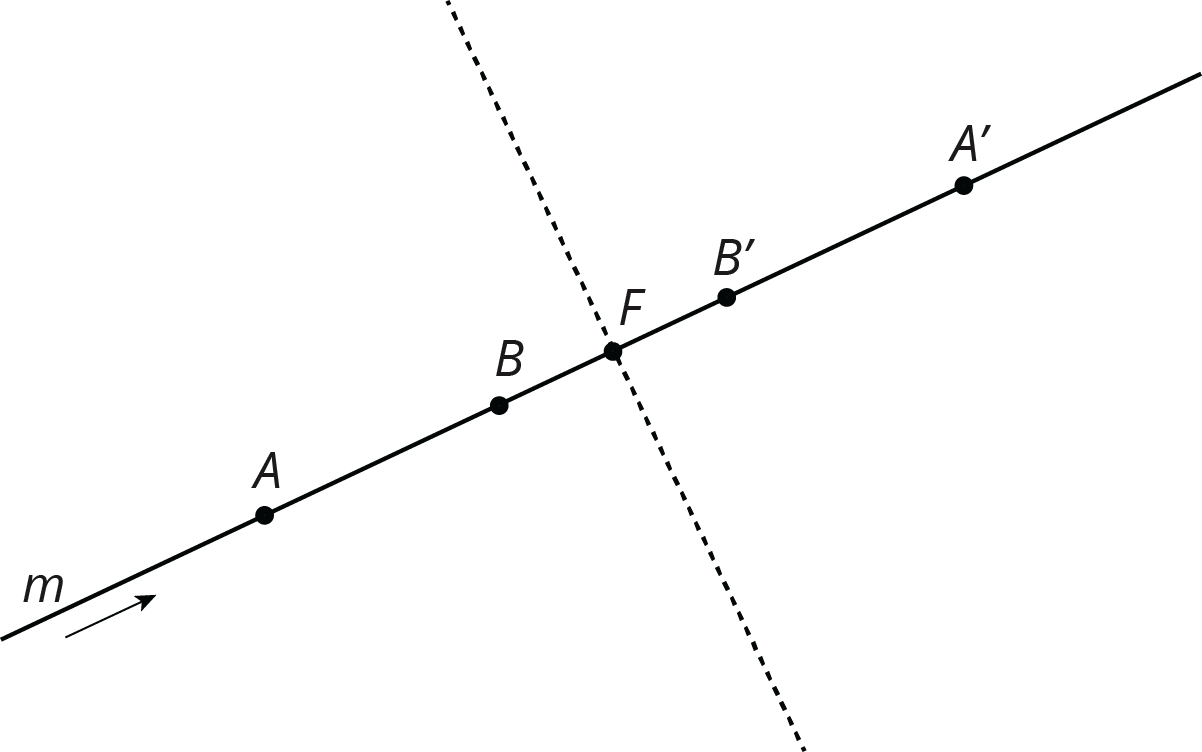
A translation parallel to the line. The arrow shows a translation of line $m$ that will take $m$ to itself.
A rotation by $180^\circ$ around any point on the line. A $180^\circ$ rotation of line $m$ around point $F$ will take $m$ to itself.
A reflection across any line perpendicular to the line. A reflection of line $m$ across the dashed line will take $m$ to itself.
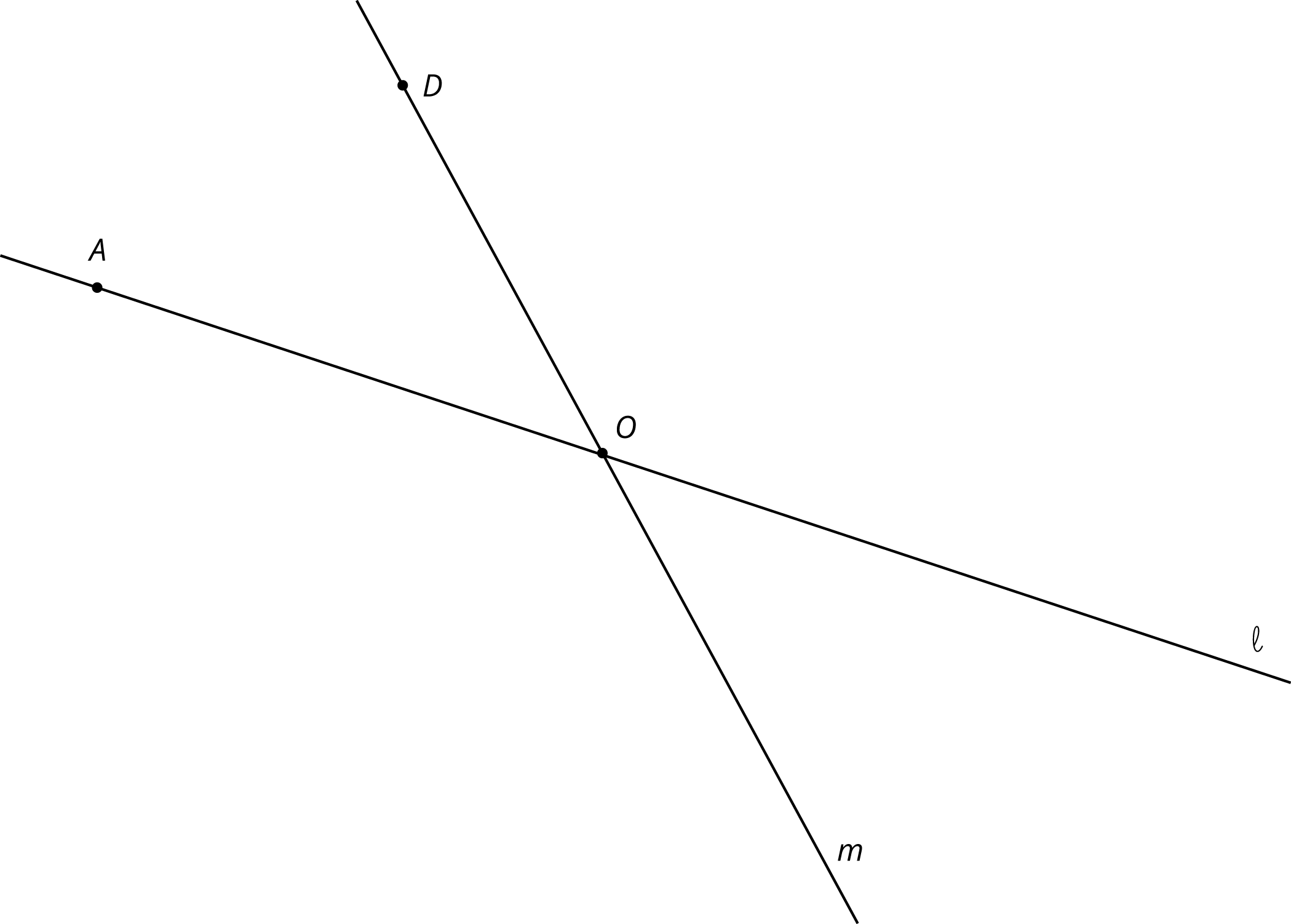
These facts let us make an important conclusion. If two lines intersect at a point, which we’ll call $O$, then a $180^\circ$ rotation of the lines with center $O$ shows that vertical angles are congruent. Here is an example:
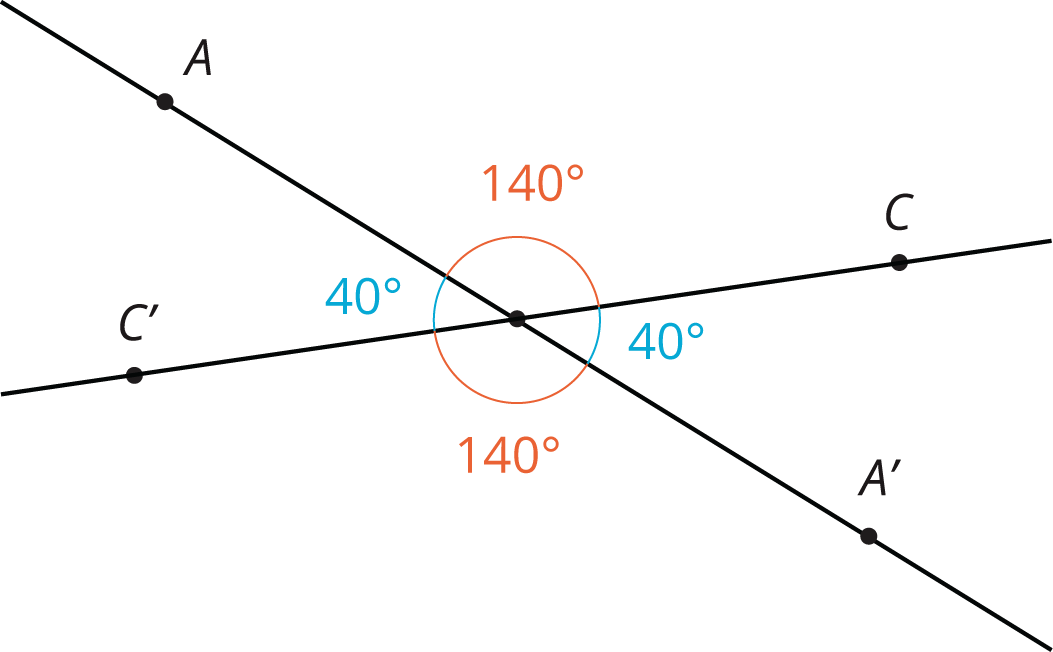
Rotating both lines by $180^\circ$ around $O$ sends angle $AOC$ to angle $A’OC’$, proving that they have the same measure. The rotation also sends angle $AOC’$ to angle $A’OC$.
A pair of vertical angles is a pair of angles that are across from each other at the point where two lines intersect. There are two pairs of vertical angles.