Lesson 1: What Influences Temperature?

Let’s see if we can predict the weather.

1.1: Temperature Changes

What factors or variables can influence the outside temperature?

  • Make a list of different factors.

  • Write a sentence for each factor describing how changing it could change the temperature.

Example: one factor is time of day. Often, after sunrise, the temperature increases, reaches a peak in the early afternoon, and then decreases.

1.2: Is Temperature a Function of Latitude?

  1. Andre and Lin are wondering if temperature is a function of latitude.

    Andre says, “I think it is, as long as we fix the time when we are measuring the temperature.”

    Lin says, “But what if you have two places with the same latitude? Look at this weather map for Washington State. Seattle and Spokane have the same latitude but different temperatures right now.”

    What do Andre and Lin mean?

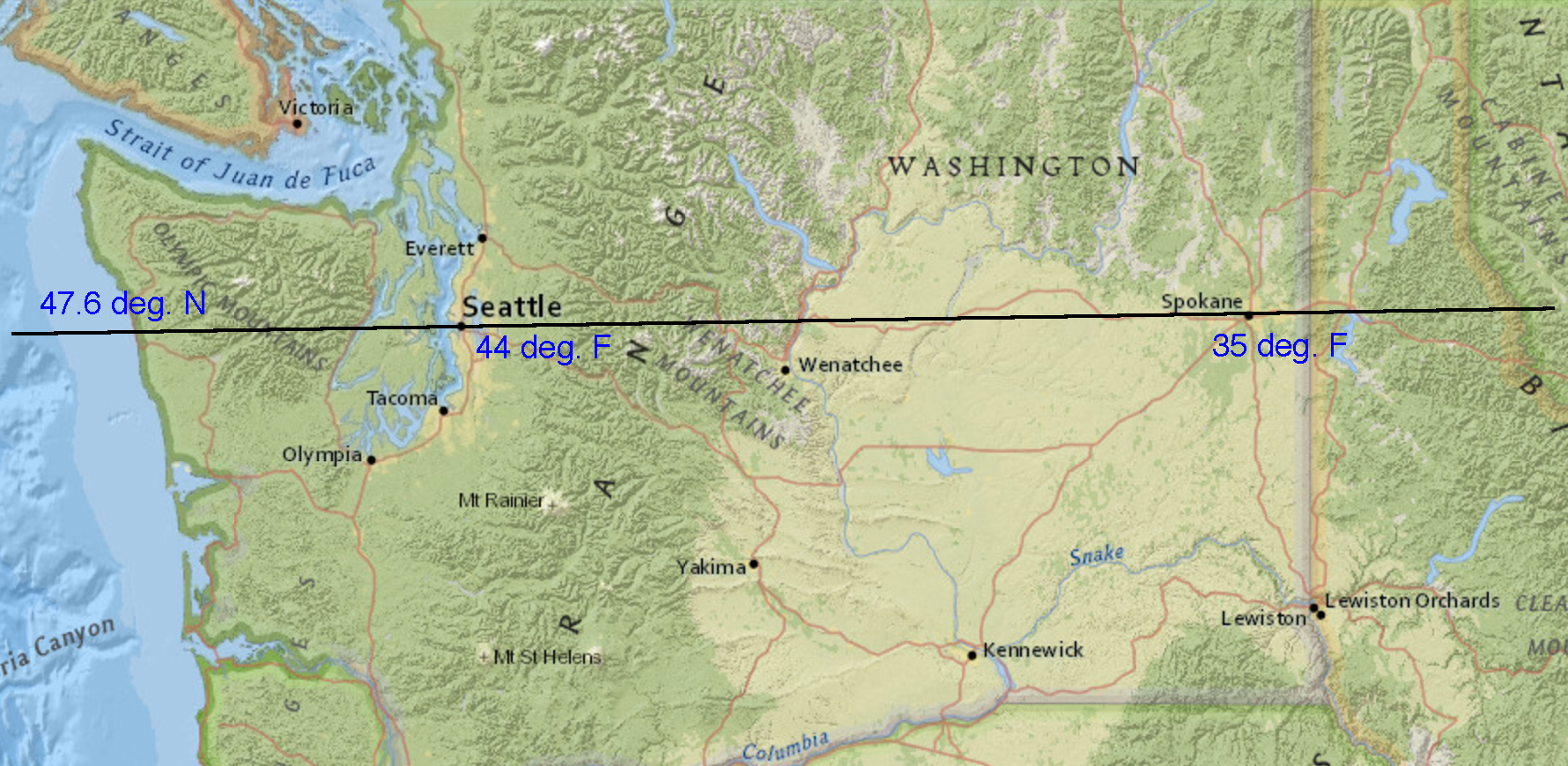    A map of Washington state. A horizontal line, labeled "forty seven point 6 degrees north" passes through two points - the cities of Seattle and Spokane. Next to Seattle, the listed temperature is "44 degrees Fahrenheit." Next to Spokane, the listed temperature is "35 degrees Fahrenheit." Map of Washington Copyright Owner: American Fact Finder License: Public Domain Via: American Fact Finder
  2. Andre and Lin are discussing whether it is possible to define latitude and temperature in a way that makes sense to talk about temperature as a function of latitude. They are considering different options. What are some advantages and disadvantages of each option?
    Here are the options: 

    1. Finding the temperature right now in cities with different latitudes.

    2. Finding the daily high temperature at cities that have different latitudes.

    3. Finding the average high temperature in a specific month, e.g., September, at cities that have different latitudes.

    4. Finding the average yearly temperature at cities that have have different latitudes.

1.3: Is There an Association Between Latitude and Temperature?

Lin and Andre decided that modeling temperature as a function of latitude doesn’t really make sense. They realized that they can ask whether there is an association between latitude and temperature.

  1. What information could they gather to determine whether temperature is related to latitude?

  2. What should they do with that information to answer the question?

1.4: California Rain

What do you notice? What do you wonder?

 

1.5: Data Snooping

Examine the data in the table.

  city latitude (degrees north) average high temperature in September (degrees F)
row 1 Atlanta, GA 33.38 82
row 2 Portland, ME 43.38 69
row 3 Boston, MA 42.22 73
row 4 Dallas, TX 32.51 88
row 5 Denver, CO 39.46 77
row 6 Edmonton, AB 53.34 62
row 7 Fairbanks, AK 64.48 55
row 8 Juneau, AK 58.22 56
row 9 Kansas City, MO 39.16 78
row 10 Lincoln, NE 40.51 77
row 11 Miami, FL 25.45 88
row 12 Minneapolis, MN 44.53 71
row 13 New York City, NY 40.38 75
row 14 Orlando, FL 28.26 90
row 15 Philadelphia, PA 39.53 78
row 16 San Antonio, TX 29.32 89
row 17 San Francisco, CA 37.37 74
row 18 Seattle, WA 47.36 69
row 19 Tampa, FL 27.57 89
row 20 Tucson, AZ 32.13 93
row 21 Yellowknife, NT  62.27 50
  1. What information does each row contain?
  2. What is the range for each variable?
  3. Do you see an association between the two variables? If so, describe the association.

1.6: Temperature vs. Latitude

  1. Make a scatter plot of the data. Describe any patterns of association that you notice.

  2. Draw a line that fits the data. Write an equation for this line.

1.7: Using a Mathematical Model

In the previous activity, you found the equation of a line to represent the association between latitude and temperature. This is a mathematical model.

  1. Use your model to predict the average high temperature in September at the following cities that were not included in the original data set:

    1. Detroit (Lat: 42.14)

    2. Albuquerque (Lat: 35.2)

    3. Nome (Lat: 64.5)

    4. Your own city (if available)

  2. Draw points that represent the predicted temperatures for each city on the scatter plot.

  3. The actual average high temperature in September in these cities were:

    • Detroit: $74^\circ$ F

    • Albuquerque: $82^\circ$ F

    • Nome: $49^\circ$ F

    • Your own city (if available):

    How well does you model predict the temperature? Compare the predicted and actual temperatures.

  4. If you added the actual temperatures for these four cities to the scatter plot, would you move your line?

  5. Are there any outliers in the data? What might be the explanation?

1.8: Interpreting a Mathematical Model

Refer to your equation for the line that models the association between latitude and temperature of the cities.

  1. What does the slope mean in the context of this situation?
  2. Find the vertical and horizontal intercepts and interpret them in the context of the situation.
  3. Can you think of a city or a location that could not be represented using this same model? Explain your thinking.