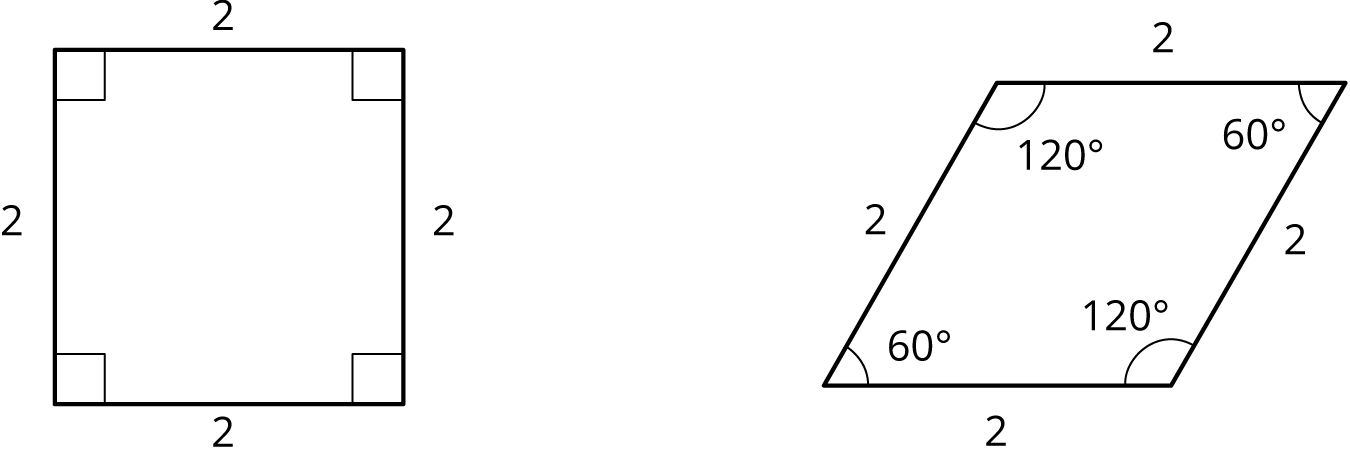Lesson 7: Similar Polygons

Let’s look at sides and angles of similar polygons.

7.1: All, Some, None: Congruence and Similarity

Choose whether each of the statements is true in all cases, in some cases, or in no cases.

  1. If two figures are congruent, then they are similar.
  2. If two figures are similar, then they are congruent.
  3. If an angle is dilated with the center of dilation at its vertex, the angle measure may change.

7.2: Are They Similar?

  1. Let’s look at a square and a rhombus.

    Priya says, “These polygons are similar because their side lengths are all the same.” Clare says, “These polygons are not similar because the angles are different.” Do you agree with either Priya or Clare? Explain your reasoning.
  2. Now, let’s look at rectangles $ABCD$ and $EFGH$.

    Jada says, “These rectangles are similar because all of the side lengths differ by 2.” Lin says, “These rectangles are similar. I can dilate $AD$ and $BC$ using a scale factor of 2 and $AB$ and $CD$ using a scale factor of 1.5 to make the rectangles congruent. Then I can use a translation to line up the rectangles.” Do you agree with either Jada or Lin? Explain your reasoning.

7.3: Find Someone Similar

Your teacher will give you a card. Find someone else in the room who has a card with a polygon that is similar but not congruent to yours. When you have found your partner, work with them to explain how you know that the two polygons are similar.

Summary

When two polygons are similar:

  • Every angle and side in one polygon has a corresponding part in the other polygon.
  • All pairs of corresponding angles have the same measure.
  • Corresponding sides are related by a single scale factor. Each side length in one figure is multiplied by the scale factor to get the corresponding side length in the other figure.

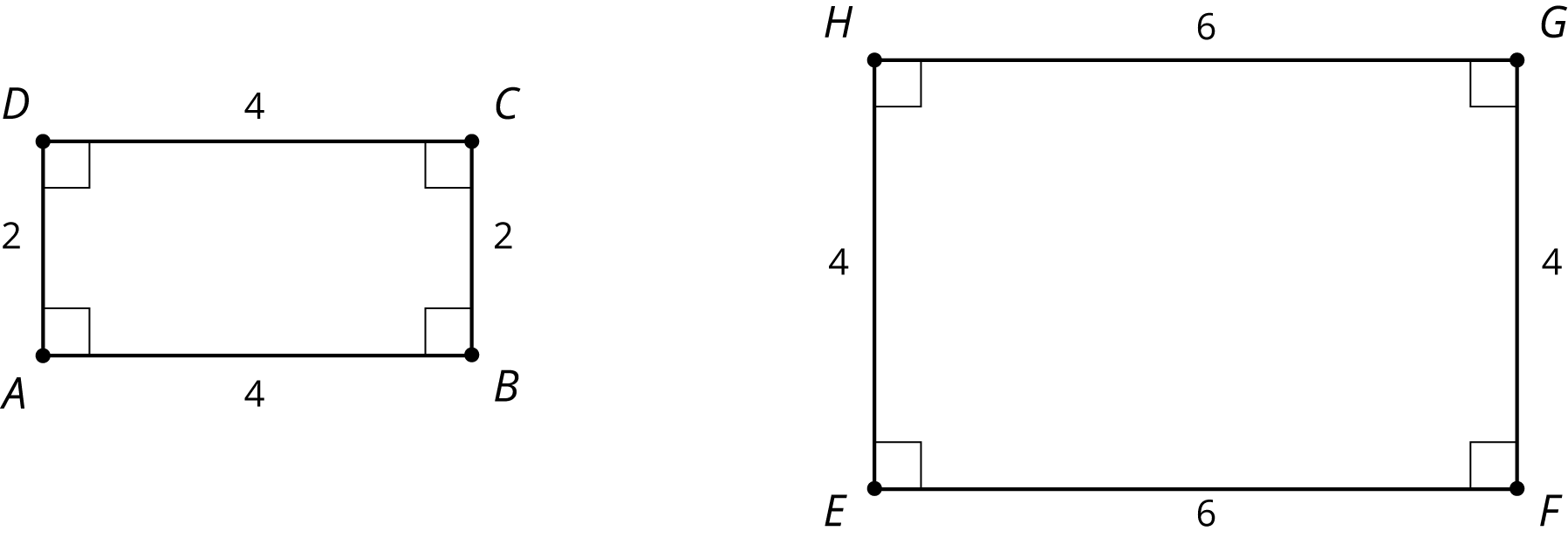
Consider the two rectangles shown here. Are they similar?

It looks like rectangles $ABCD$ and $EFGH$ could be similar, if you match the long edges and match the short edges. All the corresponding angles are congruent because they are all right angles. Calculating the scale factor between the sides is where we see that “looks like” isn’t enough to make them similar. To scale the long side $AB$ to the long side $EF$, the scale factor must be $\frac34$, because $4 \boldcdot \frac34=3$. But the scale factor to match $AD$ to $EH$ has to be $\frac23$, because $3\boldcdot \frac23=2$. So, the rectangles are not similar because the scale factors for all the parts must be the same.

Here is an example that shows how sides can correspond (with a scale factor of 1), but the quadrilaterals are not similar because the angles don’t have the same measure:

Two quadrilaterals each wides opposite sides of 2 units and 3 units. The left quadrilateral has four right angles and the right quadrilateral has opposite angle that are equal.

Practice Problems ▶