Lesson 7: Connecting Representations of Functions

Let’s connect tables, equations, graphs, and stories of functions.

7.1: Which are the Same? Which are Different?

Here are three different ways of representing functions. How are they alike? How are they different?

  1. $y = 2x$
  2. The graph of a line in the a b coordinate plane with the origin labeled “O”. On the a axis, the numbers negative 4 through 4 are indicated. On the b axis, the numbers negative 4 through 4 are indicated. The line begins in Quadrant 3, moves upward and to the right, and passes through the point negative 1 comma negative 2, passes through the origin, and the point labeled 1 comma 2.
  3. $p$ -2 -1 0 1 2 3
    $q$ 4 2 0 -2 -4 -6
 

7.2: Comparing Temperatures

The graph shows the temperature between noon and midnight in City A on a certain day.

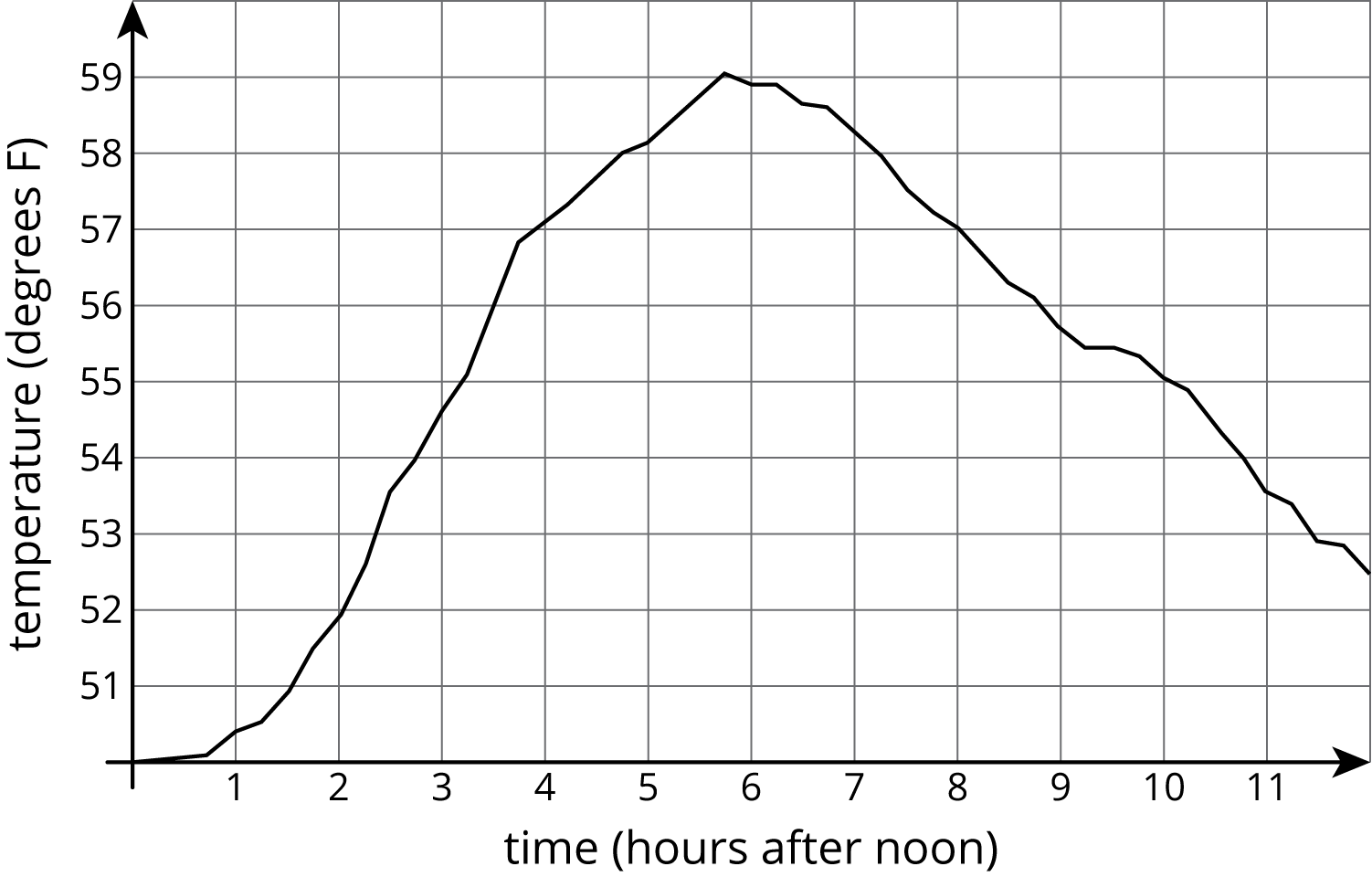
The table shows the temperature, $T$, in degrees Fahrenheit, for $h$ hours after noon, in City B. 

$h$ 1 2 3 4 5 6
$T$ 82 78 75 62 58 59
  1. Which city was warmer at 4:00 p.m.?
  2. Which city had a bigger change in temperature between 1:00 p.m. and 5:00 p.m.?
  3. How much greater was the highest recorded temperature in City B than the highest recorded temperature in City A during this time?
  4. Compare the outputs of the functions when the input is 3.

7.3: Comparing Volumes

The volume, $V$, of a cube with side length $s$ is given by the equation $V = s^3$. The graph of the volume of a sphere as a function of its radius is shown.

  1. Is the volume of a cube with side length $s=3$ greater or less than a sphere with radius 3?

  2. Estimate the radius of a sphere that has the same volume as a cube with side length 5.

  3. Compare the outputs of the two volume functions when the inputs are 2.

Here is an applet to use if you choose. Note: If you want to graph an equation with this applet, it expects you to enter $y$ as a function of $x$, so you need to use $y$ instead of $V$ and $x$ instead of $s$. 

 

7.4: It’s Not a Race

Elena’s family is driving on the freeway at 55 miles per hour.

Andre’s family is driving on the same freeway, but not at a constant speed.  The table shows how far Andre's family has traveled, $d$, in miles, every minute for 10 minutes.

$t$ 1 2 3 4 5 6 7 8 9 10
$d$ 0.9 1.9 3.0 4.1 5.1 6.2 6.8 7.4 8 9.1
  1. How many miles per minute is 55 miles per hour?
  2. Who had traveled farther after 5 minutes? After 10 minutes?
  3. How long did it take Elena’s family to travel as far as Andre’s family had traveled after 8 minutes?
  4. For both families, the distance in miles is a function of time in minutes. Compare the outputs of these functions when the input is 3.

Summary

Functions are all about getting outputs from inputs. For each way of representing a function—equation, graph, table, or verbal description—we can determine the output for a given input.

Let's say we have a function represented by the equation $y = 3x +2$ where $y$ is the dependent variable and $x$ is the independent variable. If we wanted to find the output that goes with 2, we can input 2 into the equation for $x$ and finding the corresponding value of $y$. In this case, when $x$ is 2, $y$ is 8 since $3\boldcdot 2 + 2=8$.

If we had a graph of this function instead, then the coordinates of points on the graph are the input-output pairs. So we would read the $y$-coordinate of the point on the graph that corresponds to a value of 2 for $x$. Looking at the graph of this function here, we can see the point $(2,8)$ on it, so the output is 8 when the input is 2.

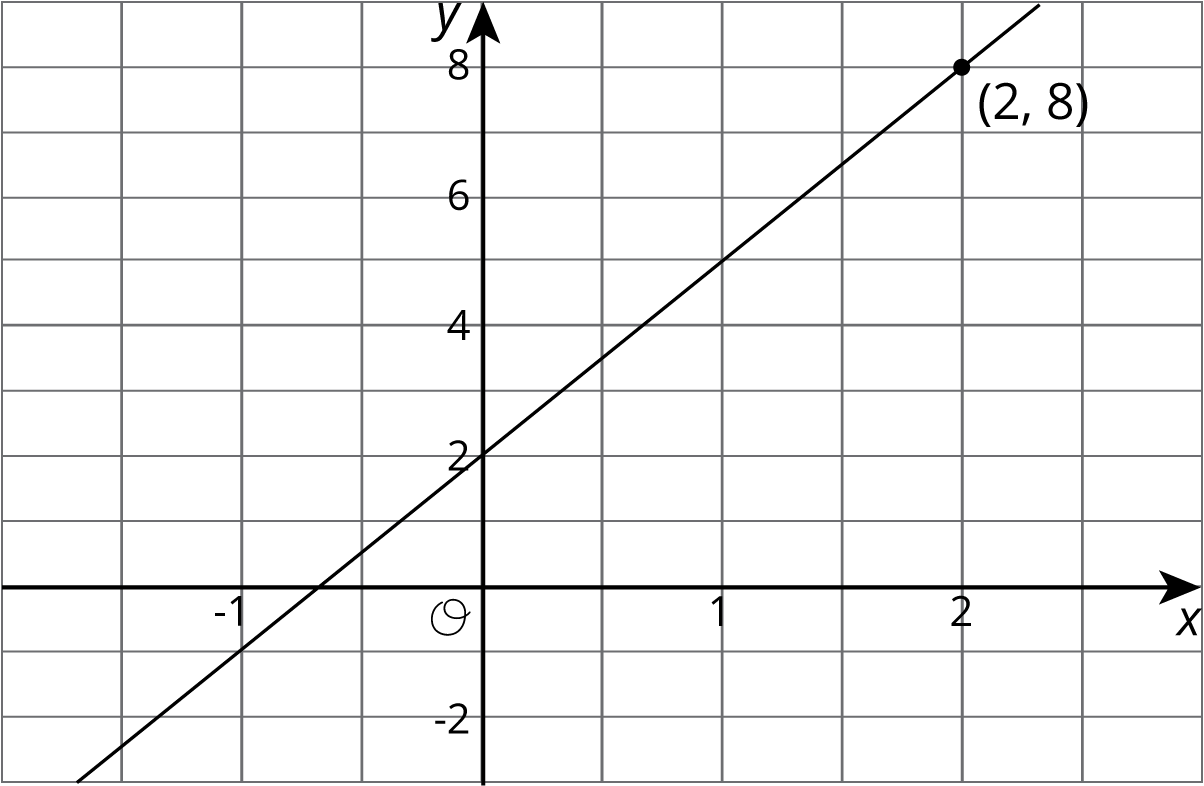
he graph of a line in the coordinate plane with the origin labeled “O”. The horizontal axis has the numbers negative 1 through 2 indicated and there are vertical gridlines between each integer. The vertical axis has the numbers negative 2 through 8, in increments of 2, indicated, and there are horizontal grid lines in between each integer. The line begins to the right of the y axis and below the x axis. It slants upward and to the right passing through the point with coordinates negative 1 comma negative 1, crosses the y axis at 2, and passes through the indicated point labeled 2 comma 8.

A table representing this function shows the input-output pairs directly (although only for select inputs).

$x$ -1 0 1 2 3
$y$ -1 2 5 8 11

Again, the table shows that if the input is 2, the output is 8.

Practice Problems ▶