- $2^5$
- $3^3$
- $4^3$
Unit 7: Practice Problem Sets
Lesson 1
Problem 1
Write each expression using an exponent:
- $1 \boldcdot 7 \boldcdot 7 \boldcdot 7 \boldcdot 7 \boldcdot 7$
- $1 \boldcdot \left(\frac{4}{5}\right) \boldcdot \left(\frac{4}{5}\right) \boldcdot \left(\frac{4}{5}\right) \boldcdot \left(\frac{4}{5}\right) \boldcdot \left(\frac{4}{5}\right)$
- $1 \boldcdot (9.3) \boldcdot (9.3) \boldcdot (9.3) \boldcdot (9.3) \boldcdot (9.3) \boldcdot (9.3) \boldcdot (9.3) \boldcdot (9.3)$
- The number of coins Jada will have on the eighth day, if Jada starts with one coin and the number of coins doubles every day. (She has two coins on the first day of the doubling.)
Problem 2
Evaluate each expression:
- $6^2$
- $\left(\frac{1}{2}\right)^4$
- $\left(\frac{1}{3}\right)^2$
Problem 3
Clare made \$160 babysitting last summer. She put the money in a savings account that pays 3% interest per year. If Clare doesn’t touch the money in her account, she can find the amount she’ll have the next year by multiplying her current amount by 1.03.
- How much money will Clare have in her account after 1 year? After 2 years?
- How much money will Clare have in her account after 5 years? Explain your reasoning.
- Write an expression for the amount of money Clare would have after 30 years if she never withdraws money from the account.
Problem 4 (from Unit 3, Lesson 1)
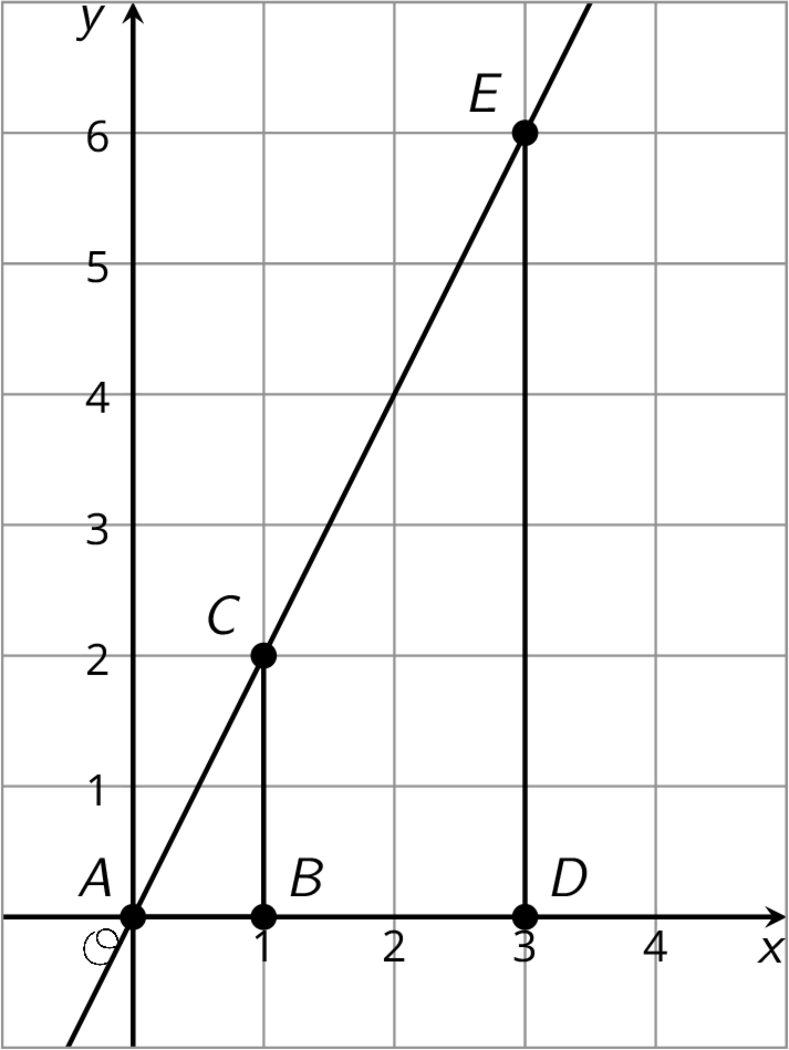
The equation $y=5,\!280x$ gives the number of feet, $y$, in $x$ miles. What does the number 5,280 represent in this relationship?
Problem 5 (from Unit 3, Lesson 5)
The points $(2, 4)$ and $(6, 7)$ lie on a line. What is the slope of the line?
- 2
- 1
- $\frac43$
- $\frac34$
Problem 6 (from Unit 2, Lesson 6)
The diagrams shows a pair of similar figures, one contained in the other. Name a point and a scale factor for a dilation that moves the larger figure to the smaller one.
Lesson 2
Problem 1
Write each expression with a single exponent:
- $10^3 \boldcdot 10^9$
- $10 \boldcdot 10^4$
- $10^{10} \boldcdot 10^7$
- $10^3 \boldcdot 10^3$
- $10^5 \boldcdot 10^{12}$
- $10^6 \boldcdot 10^6 \boldcdot 10^6$
Problem 2
A large rectangular swimming pool is 1,000 feet long, 100 feet wide, and 10 feet deep. The pool is filled to the top with water.
- What is the area of the surface of the water in the pool?
- How much water does the pool hold?
- Express your answers to the previous two questions as powers of 10.
Problem 3 (from Unit 2, Lesson 7)
Here is triangle $ABC$.
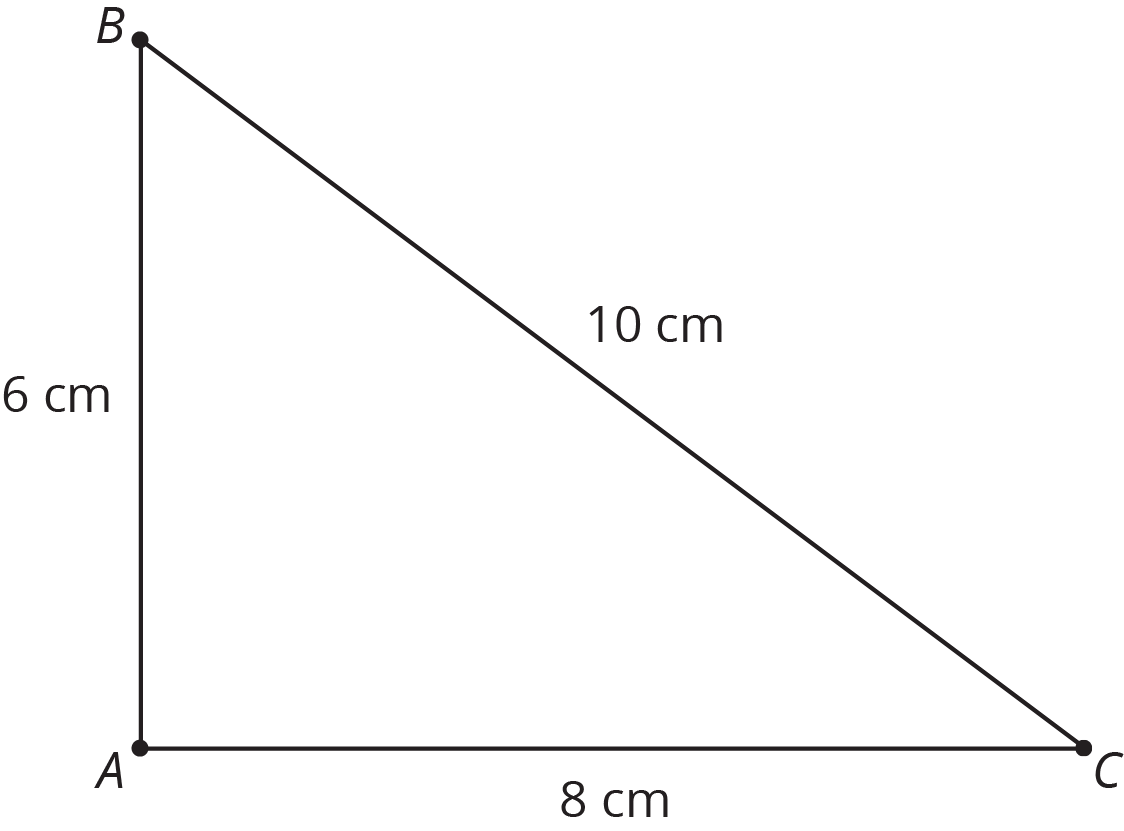
Triangle $DEF$ is similar to triangle $ABC$, and the length of $EF$ is 5 cm. What are the lengths of sides $DE$ and $DF$, in centimeters?
Problem 4 (from Unit 3, Lesson 3)
Elena and Jada distribute flyers for different advertising companies. Elena gets paid 65 cents for every 10 flyers she distributes, and Jada gets paid 75 cents for every 12 flyers she distributes.
Draw graphs on the coordinate plane representing the total amount each of them earned, $y$, after distributing $x$ flyers. Use the graph to decide who got paid more after distributing 14 flyers.

Lesson 3
Problem 1
Write each expression with a single exponent:
- $(10^7)^2$
- $(10^9)^3$
- $(10^6)^3$
- $(10^2)^3$
- $(10^3)^2$
- $(10^5)^7$
Problem 2
You have 1,000,000 number cubes, each measuring one inch on a side.
- If you stacked the cubes on top of one another to make an enormous tower, how high would they reach? Explain your reasoning.
- If you arranged the cubes on the floor to make a square, would the square fit in your classroom? What would its dimensions be? Explain your reasoning.
- If you layered the cubes to make one big cube, what would be the dimensions of the big cube? Explain your reasoning.
Problem 3 (from Unit 7, Lesson 1)
An amoeba divides to form two amoebas after one hour. One hour later, each of the two amoebas divides to form two more. Every hour, each amoeba divides to form two more.
- How many amoebas are there after 1 hour?
- How many amoebas are there after 2 hours?
- Write an expression for the number of amoebas after 6 hours.
- Write an expression for the number of amoebas after 24 hours.
- Why might exponential notation be preferable to answer these questions?
Problem 4 (from Unit 4, Lesson 15)
Elena noticed that, nine years ago, her cousin Katie was twice as old as Elena was then. Then Elena said, “In four years, I’ll be as old as Katie is now!” If Elena is currently $e$ years old and Katie is $k$ years old, which system of equations matches the story?
- \(\begin{cases}k-9=2e \\e+4=k \\ \end{cases}\)
- \(\begin{cases}2k=e-9 \\e=k+4 \\ \end{cases}\)
-
\(\begin{cases}k=2e-9 \\e+4=k+4 \\ \end{cases}\)
-
\(\begin{cases}k-9=2(e-9) \\e+4=k \\ \end{cases}\)
Lesson 4
Problem 1
Evaluate:
- $10^0$
- $\frac{10^3}{10^3}$
- $10^2 + 10^1 + 10^0$
Problem 2
Write each expression as a single power of 10.
- $\frac{10^3 \boldcdot 10^4}{10^5}$
- $(10^4) \boldcdot \frac{10^{12}}{10^7}$
- $(\frac{10^5}{10^3})^4$
- $\frac{10^4 \boldcdot 10^5 \boldcdot 10^6}{10^3 \boldcdot 10^7}$
- $\frac{(10^5)^2}{(10^2)^3}$
Problem 3
Problem 4 (from Unit 5, Lesson 3)
Bananas cost \$1.50 per pound, and guavas cost \$3.00 per pound. Kiran spends \$12 on fruit for a breakfast his family is hosting. Let $b$ be the number of pounds of bananas Kiran buys and $g$ be the number of pounds of guavas he buys.
- Write an equation relating the two variables.
- Rearrange the equation so $b$ is the independent variable.
- Rearrange the equation so $g$ is the independent variable.
Problem 5 (from Unit 3, Lesson 1)
Lin’s mom bikes at a constant speed of 12 miles per hour. Lin walks at a constant speed $\frac13$ of the speed her mom bikes. Sketch a graph of both of these relationships.
Lesson 5
Problem 1
Write with a single exponent: (ex: $\frac{1}{10} \boldcdot \frac{1}{10} = 10^{\text-2}$)
- $\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}$
- $\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}$
- $(\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10})^2$
- $(\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10})^3$
- $(10 \boldcdot 10 \boldcdot 10)^{\text-2}$
Problem 2
Write each expression as a single power of 10.
- $10^{\text-3} \boldcdot 10^{\text-2}$
- $10^4 \boldcdot 10^{\text-1}$
- $\frac{10^5}{10^7}$
- $(10^{\text-4})^5$
- $10^{\text-3} \boldcdot 10^{\text2}$
- $\frac{10^{\text-9}}{10^5}$
Problem 3
Select all of the following that are equivalent to $\frac{1}{10,000}$:
- $(10,\!000)^{\text-1}$
- $(\text{-}10,\!000)$
- $(100)^{\text-2}$
- $(10)^{\text-4}$
- $(\text{-}10)^2$
Problem 4 (from Unit 3, Lesson 2)
Match each equation to the situation it describes. Explain what the constant of proportionality means in each equation.
Equations:
- $y=3x$
- $\frac12x=y$
- $y=3.5x$
- $y=\frac52x$
Situations:
- A dump truck is hauling loads of dirt to a construction site. After 20 loads, there are 70 square feet of dirt.
- I am making a water and salt mixture that has 2 cups of salt for every 6 cups of water.
- A store has a “4 for $10” sale on hats.
- For every 48 cookies I bake, my students get 24.
Problem 5 (from Unit 2, Lesson 8)
-
Explain why triangle $ABC$ is similar to $EDC$.
- Find the missing side lengths.
Lesson 6
Problem 1
Priya says “I can figure out $5^0$ by looking at other powers of 5. $5^3$ is 125, $5^2$ is 25, then $5^1$ is 5.”
- What pattern do you notice?
- If this pattern continues, what should be the value of $5^0$? Explain how you know.
- If this pattern continues, what should be the value of $5^{\text-1}$? Explain how you know.
Problem 2
Select all the expressions that are equivalent to $4^{\text-3}$.
- -12
- $2^{\text-6}$
- $\frac{1}{4^3}$
- $\left(\frac{1}{4}\right) \boldcdot \left(\frac{1}{4}\right) \boldcdot \left(\frac{1}{4}\right)$
- 12
- $(\text-4) \boldcdot (\text-4) \boldcdot (\text-4)$
- $\frac{8^{\text-1}}{2^2}$
Problem 3
Write each expression using a single exponent.
- $\frac{5^3}{5^6}$
- $(14^3)^6$
- $8^3 \boldcdot 8^6$
- $\frac{16^6}{16^3}$
- $(21^3)^{\text-6}$
Problem 4 (from Unit 5, Lesson 6)
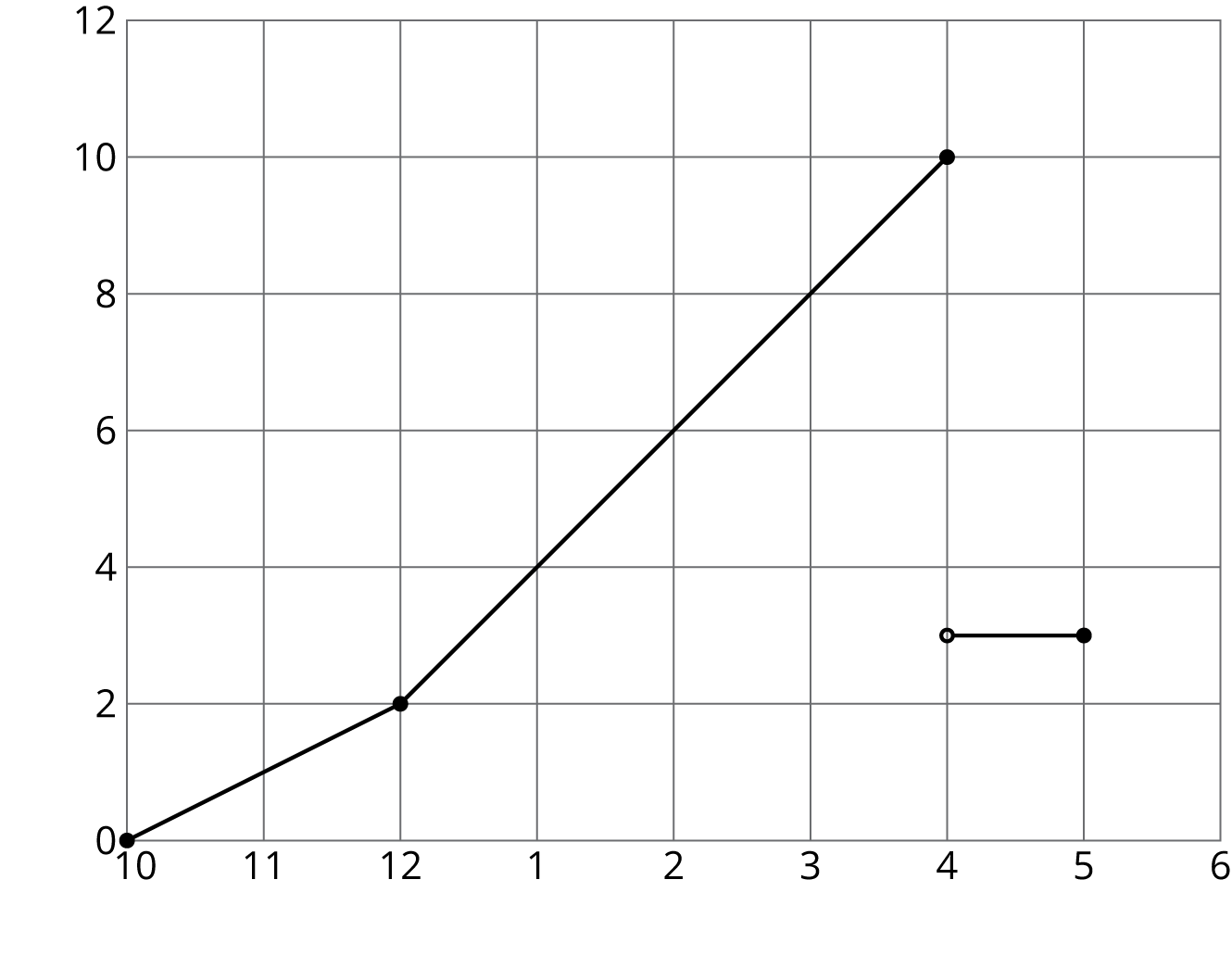
Andre sets up a rain gauge to measure rainfall in his back yard. On Tuesday, it rains off and on all day.
- He starts at 10 a.m. with an empty gauge when it starts to rain.
- Two hours later, he checks, and the gauge has 2 cm of water in it.
- It starts raining even harder, and at 4 p.m., the rain stops, so Andre checks the rain gauge and finds it has 10 cm of water in it.
- While checking it, he accidentally knocks the rain gauge over and spills most of the water, leaving only 3 cm of water in the rain gauge.
- When he checks for the last time at 5 p.m., there is no change.
Graph A
Graph B
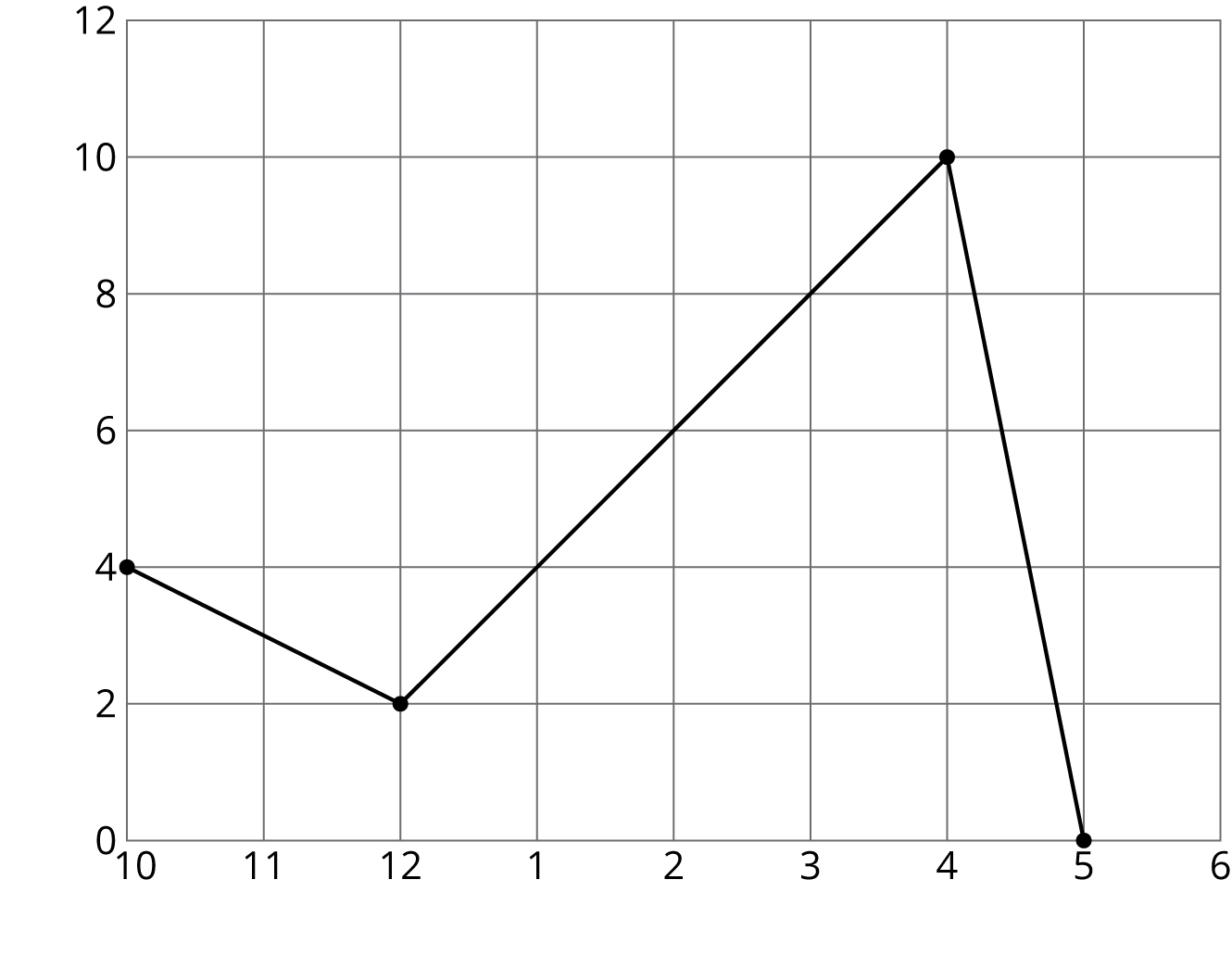
- Which of the two graphs could represent Andre’s story? Explain your reasoning.
- Label the axes of the correct graph with appropriate units.
- Use the graph to determine how much total rain fell on Tuesday.
Lesson 7
Problem 1
Write with a single exponent:
- $\frac{7^6}{7^2}$
- $(11^4)^5$
- $4^2 \boldcdot 4^6$
- $6 \boldcdot 6^8$
- $(12^2)^7$
- $\frac{3^{10}}{3}$
- $(0.173)^9 \boldcdot (0.173)^2$
- $\frac{0.87^5}{0.87^3}$
- $\frac{(\frac{5}{2})^8}{(\frac{5}{2})^6}$
Problem 2
Noah says that $2^4 \boldcdot 3^2 = 6^6$. Tyler says that $2^4 \boldcdot 4^2 = 16^2$.
- Do you agree with Noah? Explain or show your reasoning.
- Do you agree with Tyler? Explain or show your reasoning.
Lesson 8
Problem 1
Select all the true statements:
- $2^8 \boldcdot 2^9 = 2^{17}$
- $8^2 \boldcdot 9^2 = 72^2$
- $8^2 \boldcdot 9^2 = 72^4$
- $2^8 \boldcdot 2^9 = 4^{17}$
Problem 2
Find $x$, $y$, and $z$ if $(3 \boldcdot 5)^4 \boldcdot (2 \boldcdot 3)^5 \boldcdot (2 \boldcdot 5)^7 = 2^x \boldcdot 3^y \boldcdot 5^z$.
Problem 3
Han found a way to compute complicated expressions more easily. Since $2 \boldcdot 5 = 10$, he looks for pairings of 2s and 5s that he knows equal 10. For example, $3 \boldcdot 2^4 \boldcdot 5^5 = 3 \boldcdot 2^4 \boldcdot 5^4 \boldcdot 5 = (3 \boldcdot 5) \boldcdot (2 \boldcdot 5)^4 = 15 \boldcdot 10^4 = 150,\!000.$ Use Han's technique to compute the following:
- $2^4 \boldcdot 5 \boldcdot (3 \boldcdot 5)^3$
- $\frac{2^3 \boldcdot 5^2 \boldcdot (2 \boldcdot 3)^2 \boldcdot (3 \boldcdot 5)^2}{3^2}$
Problem 4 (from Unit 5, Lesson 8)
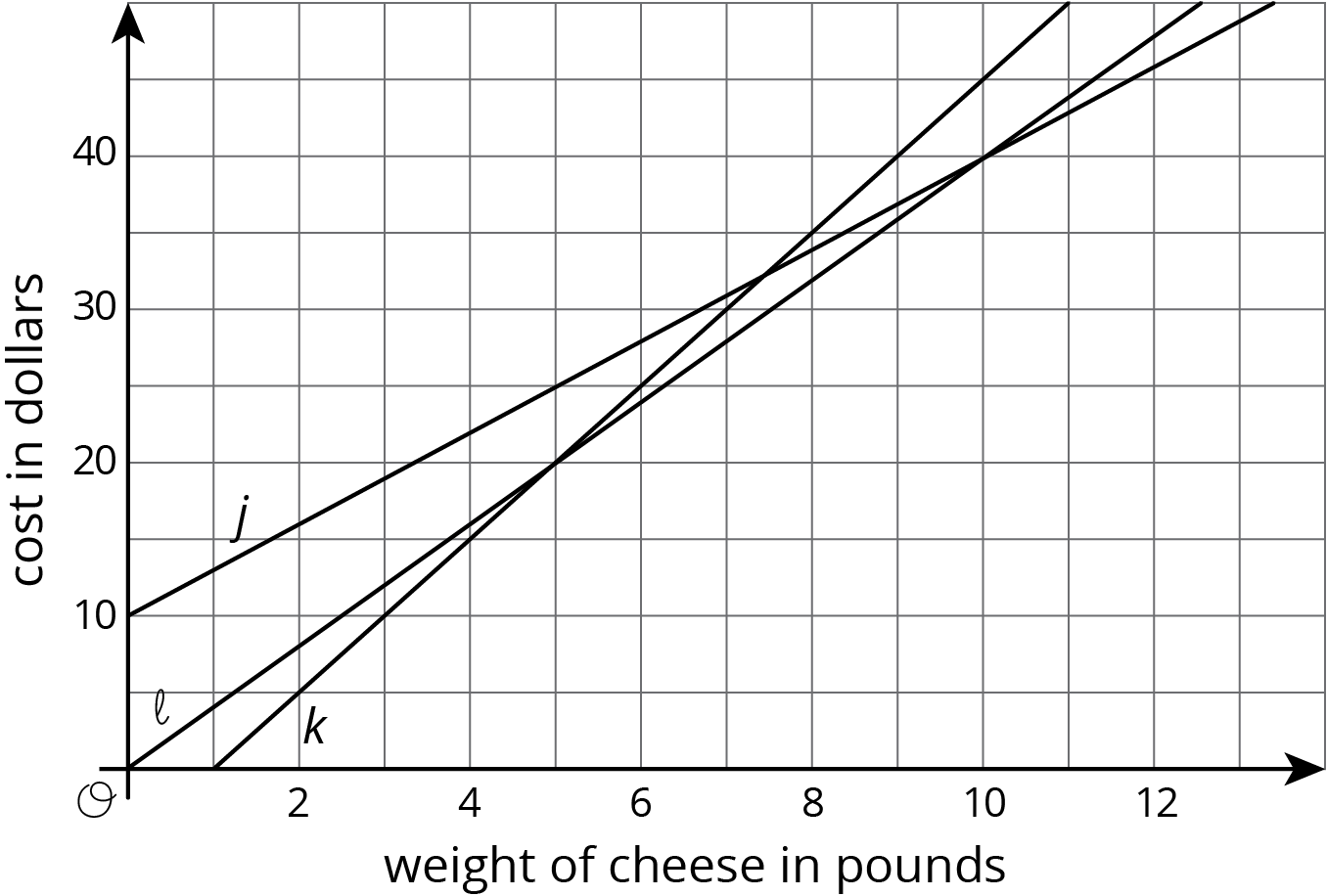
The cost of cheese at three stores is a function of the weight of the cheese. The cheese is not prepackaged, so a customer can buy any amount of cheese.
-
Store A sells the cheese for $a$ dollars per pound.
-
Store B sells the same cheese for $b$ dollars per pound and a customer has a coupon for \$5 off the total purchase at that store.
-
Store C is an online store, selling the same cheese at $c$ dollar per pound, but with a \$10 delivery fee.
This graph shows the price functions for stores A, B, and C.
-
Match Stores A, B, and C with Graphs $j$, $k$, and $\ell$.
-
How much does each store charge for the cheese per pound?
-
How many pounds of cheese does the coupon for Store B pay for?
-
Which store has the lowest price for a half a pound of cheese?
-
If a customer wants to buy 5 pounds of cheese for a party, which store has the lowest price?
-
How many pounds would a customer need to order to make Store C a good option?
Lesson 9
Problem 1
Match each number to its name.
- 1,000,000
- 0.01
- 1,000,000,000
- 0.000001
- 0.001
- 10,000
- One hundredth
- One thousandth
- One millionth
- Ten thousand
- One million
- One billion
Problem 2
Write each expression as a multiple of a power of 10:
- 42,300
- 2,000
- 9,200,000
- Four thousand
- 80 million
- 32 billion
Problem 3
Each statement contains a quantity. Rewrite each quantity using a power of 10.
- There are about 37 trillion cells in an average human body.
- The Milky Way contains about 300 billion stars.
- A sharp knife is 23 millionths of a meter thick at its tip.
- The wall of a certain cell in the human body is 4 nanometers thick. (A nanometer is one billionth of a meter.)
Problem 4 (from Unit 5, Lesson 20)
A fully inflated basketball has a radius of 12 cm. Your basketball is only inflated halfway. How many more cubic centimeters of air does your ball need to fully inflate? Express your answer in terms of $\pi$. Then estimate how many cubic centimeters this is by using 3.14 to approximate $\pi$.
Problem 5 (from Unit 4, Lesson 5)
Solve each of these equations. Explain or show your reasoning.
$2(3-2c) = 30$
$3x-2=7-6x$
$31=5(b-2)$
Problem 6 (from Unit 3, Lesson 10)
Graph the line going through $(\text-6,1)$ with a slope of $\frac {\text{-}2}{3}$ and write its equation. 
Lesson 10
Problem 1
Find three different ways to write the number 437,000 using powers of 10.
Problem 2
For each pair of numbers below, circle the number that is greater. Estimate how many times greater.
$17 \boldcdot 10^8$ or $4 \boldcdot 10^8$
$2 \boldcdot 10^6$ or $7.839 \boldcdot 10^6$
$42 \boldcdot 10^7$ or $8.5 \boldcdot 10^8$
Problem 3
What number is represented by point $A$? Explain or show how you know.
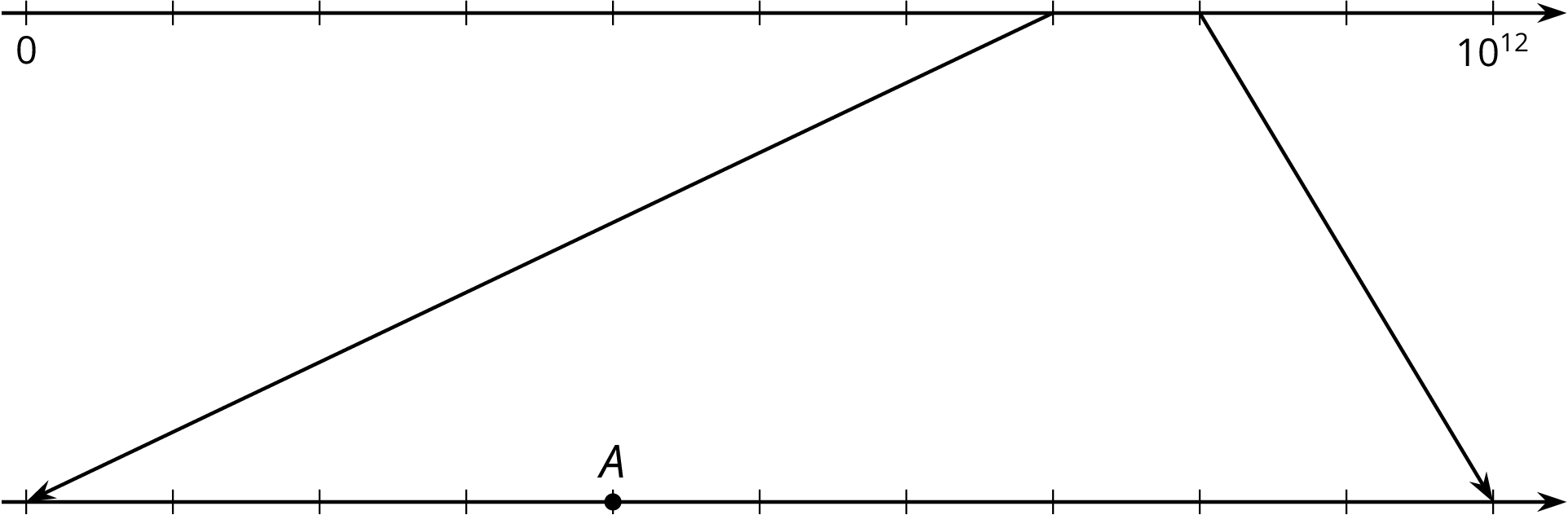
Problem 4 (from Unit 6, Lesson 7)
Here is a scatter plot that shows the number of points and assists by a set of hockey players. Select all the following that describe the association in the scatter plot:
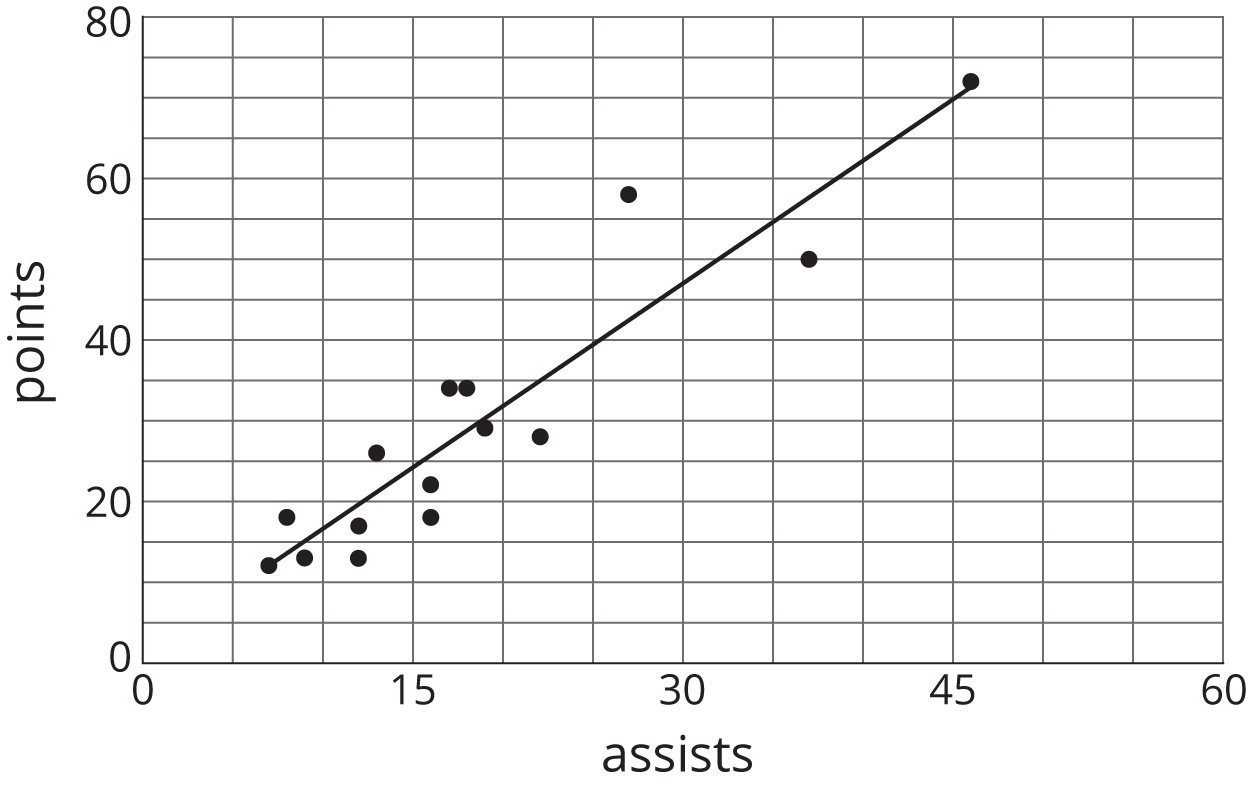
- Linear association
- Non-linear association
- Positive association
- Negative association
- No association
Problem 5 (from Unit 5, Lesson 5)
Here is the graph of days and the predicted number of hours of sunlight, $h$, on the $d$-th day of the year.

-
Is hours of sunlight a function of days of the year? Explain how you know.
-
For what days of the year is the number of hours of sunlight increasing? For what days of the year is the number of hours of sunlight decreasing?
-
Which day of the year has the greatest number of hours of sunlight?
Lesson 11
Problem 1
Select all the expressions that are equal to $4 \boldcdot 10^{\text-3}$:
- $4 \boldcdot (\frac{1}{10}) \boldcdot (\frac{1}{10}) \boldcdot (\frac{1}{10})$
- $4 \boldcdot (\text{-}10) \boldcdot (\text{-}10) \boldcdot (\text{-}10)$
- $4 \boldcdot 0.001$
- $4 \boldcdot 0.0001$
- $0.004$
- $0.0004$
Problem 2
Write each expression as a multiple of a power of 10:
- 0.04
- 0.072
- 0.0000325
- Three thousandths
- 23 hundredths
- 729 thousandths
- 41 millionths
Problem 3 (from Unit 3, Lesson 9)
A family sets out on a road trip to visit their cousins. They travel at a steady rate. The graph shows the distance remaining to their cousins' house for each hour of the trip.
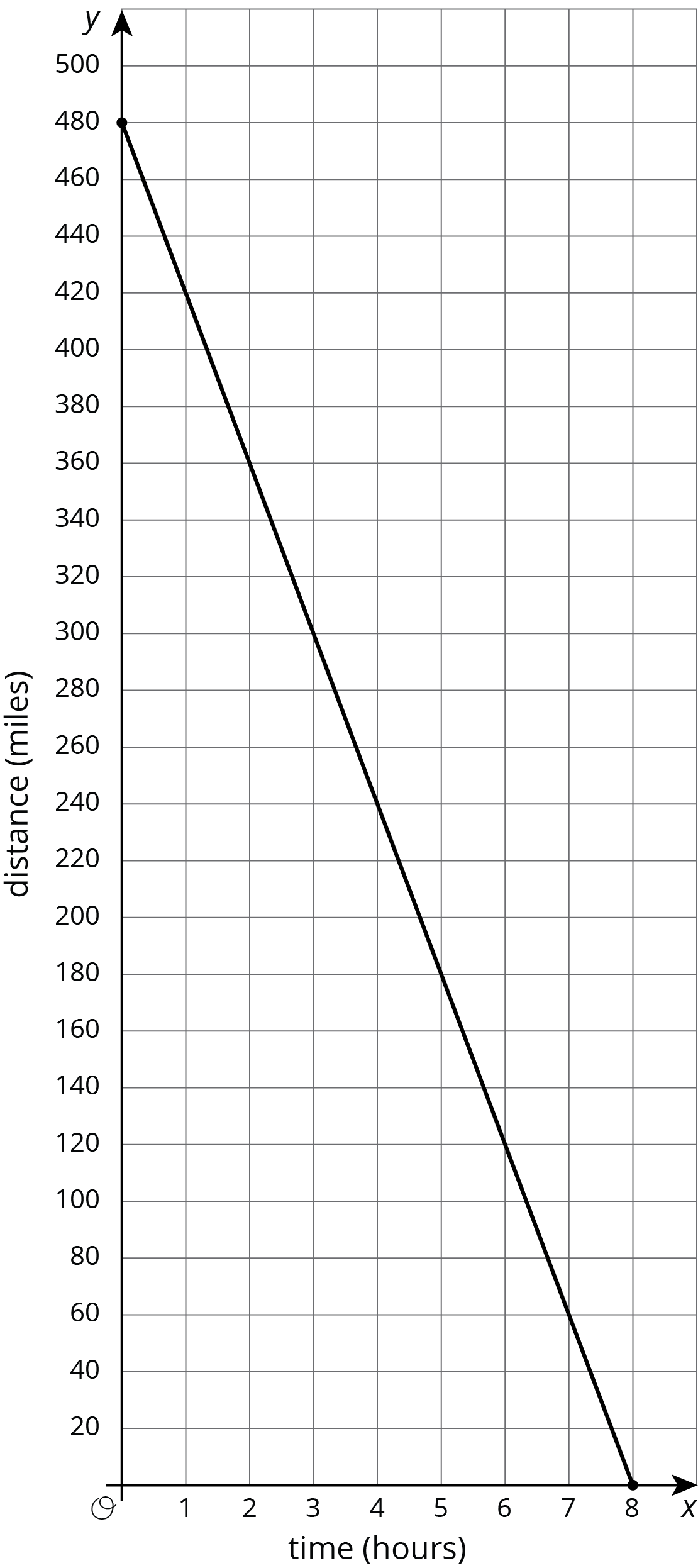
- How fast are they traveling?
- Is the slope positive or negative? Explain how you know and why that fits the situation.
- How far is the trip and how long did it take? Explain how you know.
Lesson 12
Problem 1
Which is larger: the number of meters across the Milky Way, or the number of cells in all humans? Explain or show your reasoning.
Some useful information:
- The Milky Way is about 100,000 light years across.
- There are about 37 trillion cells in a human body.
- One light year is about $10^{16}$ meters.
- The world population is about 7 billion.
Problem 2 (from Unit 6, Lesson 5)
Ecologists measure the body length and wingspan of 127 butterfly specimens caught in a single field.
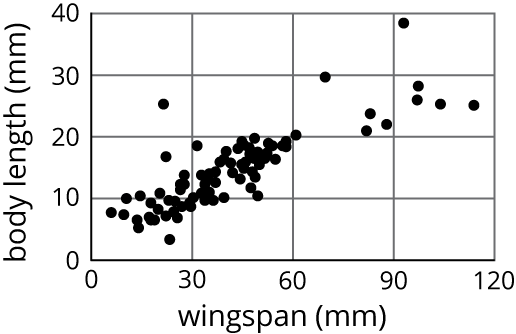
- Draw a line that you think is a good fit for the data.
- Write an equation for the line.
- What does the slope of the line tell you about the wingspans and lengths of these butterflies?
Problem 3 (from Unit 4, Lesson 5)
Diego was solving an equation, but when he checked his answer, he saw his solution was incorrect. He knows he made a mistake, but he can’t find it. Where is Diego’s mistake and what is the solution to the equation?
\begin{align} \text-4(7-2x)=3(x+4)\\ \text-28-8x=3x+12\\ \text-28=11x+12\\ \text-40=11x\\ \frac {\text{-}40}{11}=x\ \end{align}
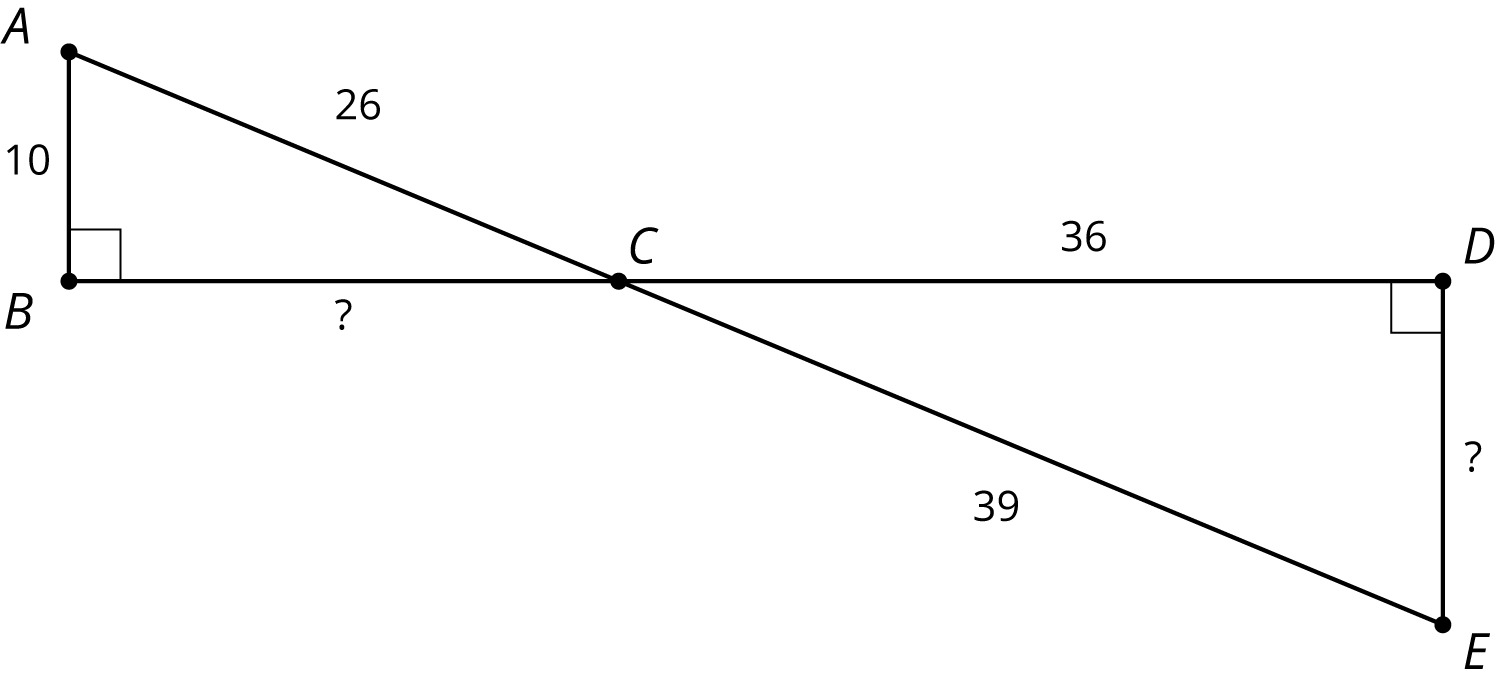
Problem 4 (from Unit 2, Lesson 7)
The two triangles are similar. Find $x$.

Lesson 13
Problem 1
Write each number in scientific notation.
- 14,700
- 0.00083
- 760,000,000
- 0.038
- 0.38
- 3.8
- 3,800,000,000,000
- 0.0000000009
Problem 2
Perform the following calculations. Express your answers in scientific notation.
- $(2 \times 10^5) + (6 \times 10^5)$
- $(4.1 \times 10^7) \boldcdot 2$
- $(1.5 \times 10^{11}) \boldcdot 3$
- $(3 \times 10^3)^2$
- $(9 \times 10^6) \boldcdot (3 \times 10^6)$
Problem 3
Jada is making a scale model of the solar system. The distance from Earth to the moon is about $2.389 \times 10^5$ miles. The distance from Earth to the sun is about $9.296 \times 10^7$ miles. She decides to put Earth on one corner of her dresser and the moon on another corner, about a foot away. Where should she put the sun?
- On a windowsill in the same room?
- In her kitchen, which is down the hallway?
- A city block away?
Explain your reasoning.
Problem 4 (from Unit 4, Lesson 12)
Here is the graph for one equation in a system of equations.
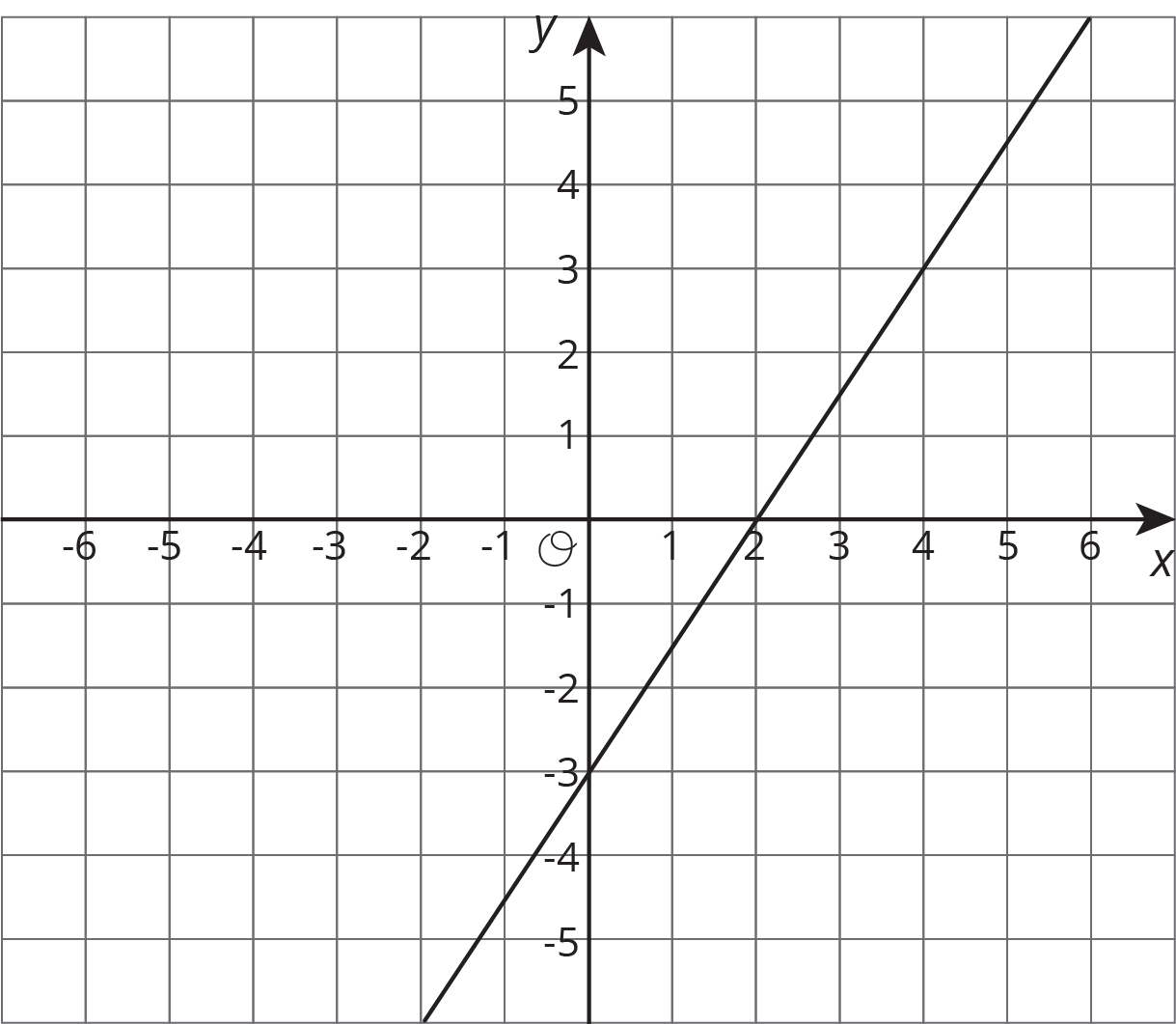
- Write a second equation for the system so it has infinitely many solutions.
- Write a second equation whose graph goes through $(0,2)$ so that the system has no solutions.
- Write a second equation whose graph goes through $(2,2)$ so that the system has one solution at $(4,3)$.
Lesson 14
Problem 1
Evaluate each expression. Use scientific notation to express your answer.
- $(1.5 \times 10^2) (5 \times 10^{10})$
- $\frac{4.8 \times 10^{\text-8}}{3 \times 10^{\text-3}}$
- $(5 \times 10^8) (4 \times 10^3)$
- $(7.2 \times 10^3) \div (1.2 \times 10^5)$
Problem 2
How many bucketloads would it take to bucket out the world’s oceans? Write your answer in scientific notation.
Some useful information:
- The world’s oceans hold roughly $1.4 \times 10^{9}$ cubic kilometers of water.
- A typical bucket holds roughly 20,000 cubic centimeters of water.
- There are $10^{15}$ cubic centimeters in a cubic kilometer.
Problem 3 (from Unit 5, Lesson 5)
The graph represents the closing price per share of stock for a company each day for 28 days.

- What variable is represented on the horizontal axis?
- In the first week, was the stock price generally increasing or decreasing?
- During which period did the closing price of the stock decrease for at least 3 days in a row?
Problem 4 (from Unit 3, Lesson 11)
Write an equation for the line that passes through $(\text- 8.5, 11)$ and $(5, \text- 2.5)$.
Problem 5 (from Unit 2, Lesson 6)
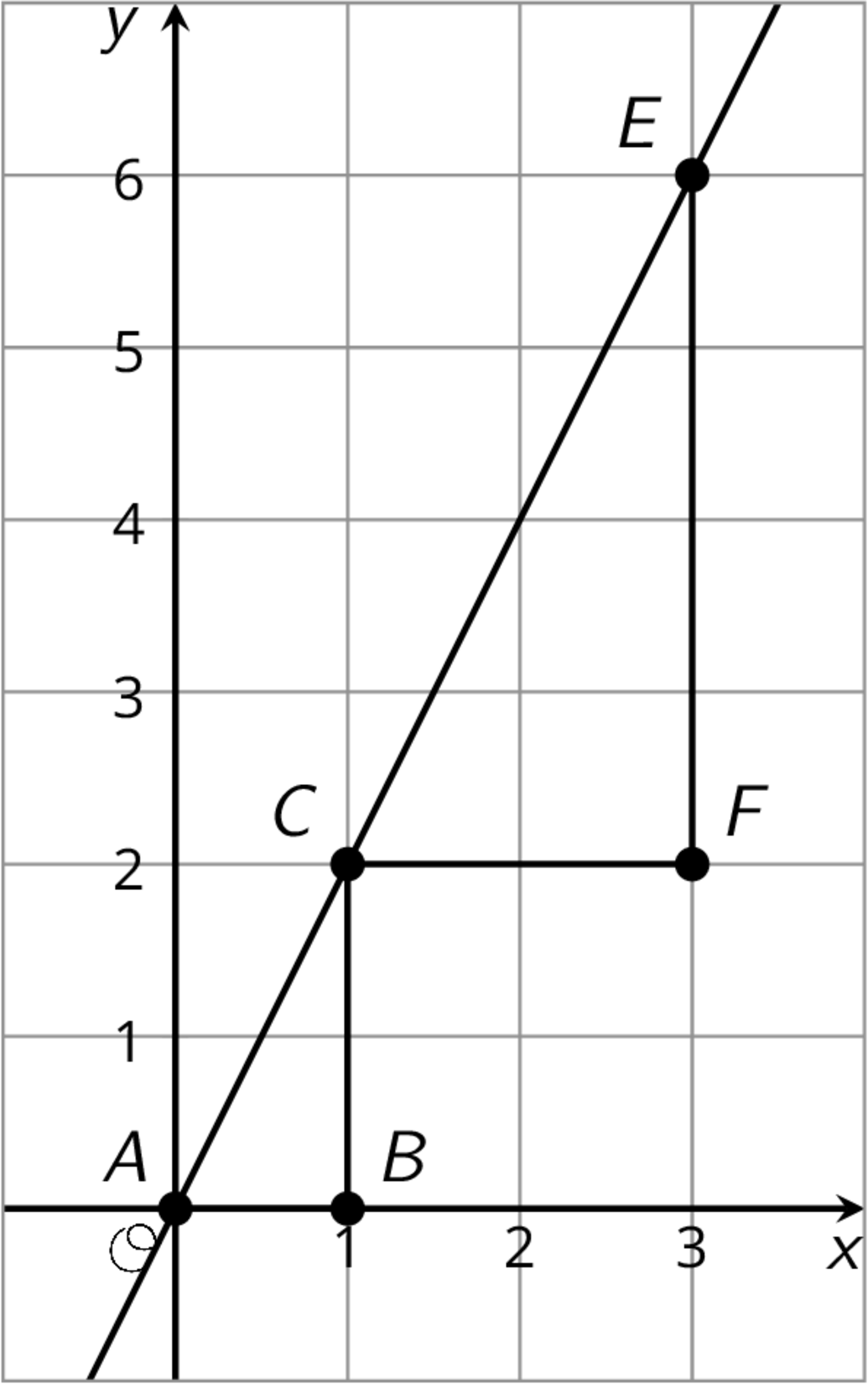
Explain why triangle $ABC$ is similar to triangle $CFE$.
Lesson 15
Problem 1
Evaluate each expression, giving the answer in scientific notation:
- $5.3 \times 10^4 + 4.7 \times 10^4$
- $3.7 \times 10^6 - 3.3 \times 10^6$
- $4.8 \times 10^{\text-3} + 6.3 \times 10^{\text-3}$
- $6.6 \times 10^{\text-5} - 6.1 \times 10^{\text-5}$
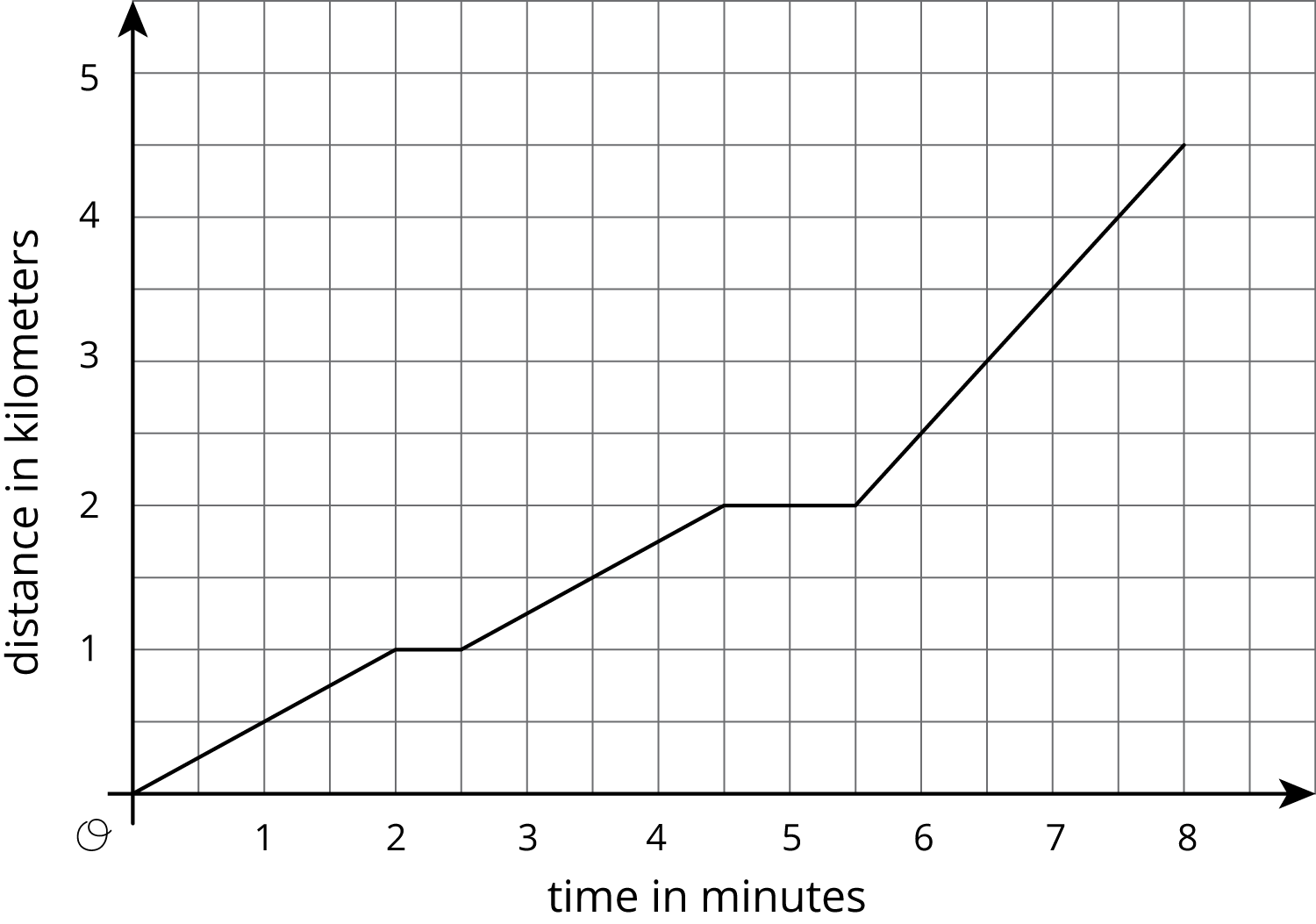
Problem 2 (from Unit 5, Lesson 10)
- Write a scenario that describes what is happening in the graph.
- What is happening at 5 minutes?
- What does the slope of the line between 6 and 8 minutes mean?
Problem 3 (from Unit 4, Lesson 10)
Apples cost \$1 each. Oranges cost \$2 each. You have \$10 and want to buy 8 pieces of fruit. One graph shows combinations of apples and oranges that total to \$10. The other graph shows combinations of apples and oranges that total to 8 pieces of fruit.
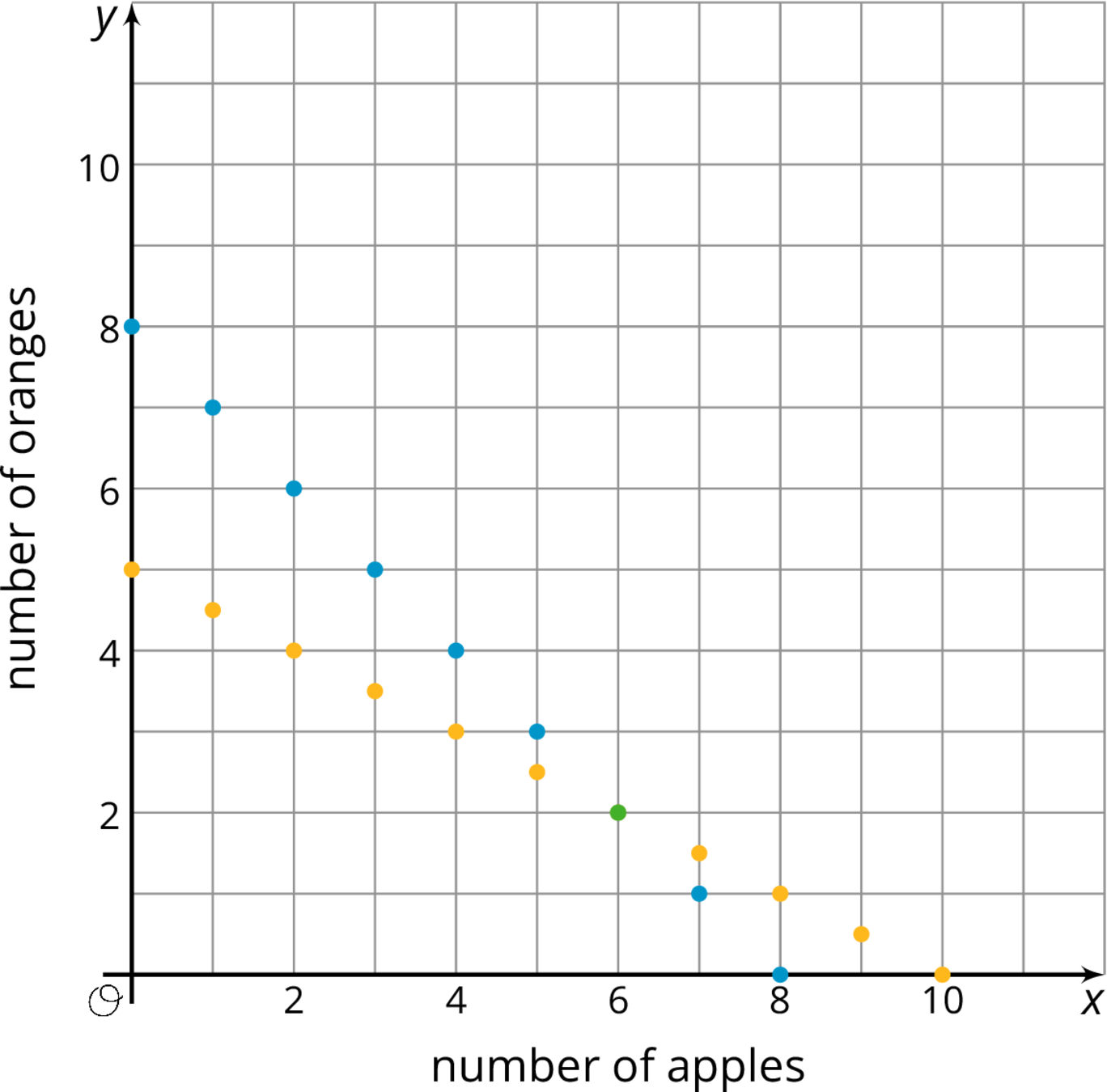
-
Name one combination of 8 fruits shown on the graph that whose cost does not total to \$10.
-
Name one combination of fruits shown on the graph whose cost totals to \$10 that are not 8 fruits all together.
-
How many apples and oranges would you need to have 8 fruits that cost \$10 at the same time?
Problem 4 (from Unit 4, Lesson 5)
Solve each equation and check your solution.
$\text-2(3x-4)=4(x+3)+6$
$\frac12(z+4)-6=\text-2z+8$
$4w-7=6w+31$
Lesson 16
No practice problems for this lesson.